Sabendo que o ponto crítico do sistema abaixo é , determine o retrato de fase e qual tipo de ponto é o ponto crítico.
Passo 1
O sistema já está na forma matricial, então só precisamos fazer os autovalores de para achar seu retrato de fases.
A primeira coisa que devemos fazer é identificar o valor da matriz
Passo 2
Agora temos que achar o autovalores de .
Lembra é só fazer
Esse é o caso de autovalores iguais, aqui vai ser uma situação onde precisamos achar seus autovetores, porque se tivermos diretos é uma coisa se tivermos direto e depois ter que resolver aquela equação auxiliar vai ser diferente o retrato de fase.
Passo 3
Agora temos que achar os autoespaços associados, para isso vamos ter
Vamos ter
E o autovetor associado vai ser
Podemos tirar esse
Agora vimos que só rola um vetor, precisamos achar o outro autovetor usando
Vamos fazer
Então
Isso deixa a equação
O auto vetor vai ser
Essa parte com vamos ignorar porque já é o outro autovetor, então
Beleza agora conseguimos fazer um esboço melhor, aqui temos que achar o segundo porque precisamos saber como é a orientação dos dois para pode deixar direitinho o retrato de fases.
Passo 4
O retrato de fases vai ser
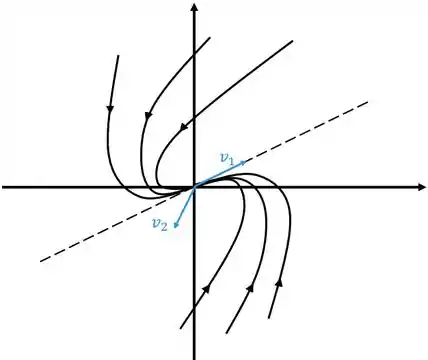
Neste caso o ponto crítico é chamado de nó impróprio.
Resposta
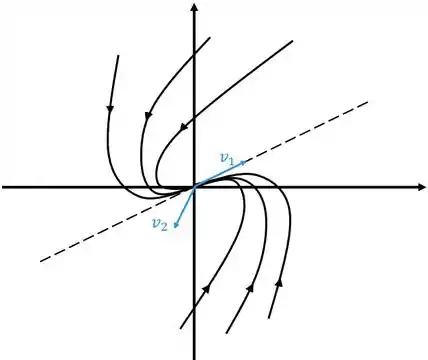
Neste caso o ponto crítico é chamado de nó impróprio.