Considere o sistema .

a) Esboce o retrato de fase e classifique a singularidade (0,0).

b) Ache a solução geral do sistema onde:

c) Ache a solução do sistema da letra (b) com condição inicial

Para resolver a equação do segundo grau, usamos a fórmula de bhaskara e ficamos com:

Ou seja, a matriz possui autovalores complexos com a parte real diferente de zero e negativa

Então como a matriz possui autovalores da forma:

Com e .

Temos que o retrato de fase é uma espiral se aproximando da origem como na figura abaixo:

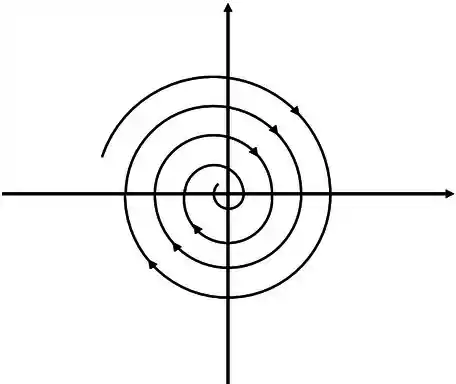
E a singularidade é classificada como estável ou atrator.

b) Queremos resolver o sistema linear

A solução geral desse sistema é dada por:

Onde é a solução do sistema linear homogêneo e é a solução particular.

Primeiro, vamos achar a solução homogênea, que tem a forma de:

Onde, é a matriz identidade e são constantes arbitrárias.

Então a nossa missão é achar o e o .

Para isso, temos que saber os autovalores da matriz

Mas já achamos eles na letra (a). Eles são:

Como os autovalores são complexos, o sistema satisfeito por e é

Substituindo os valores, temos

Subtraindo as duas, ficamos com:

E portanto,

Então a solução homogênea do sistema linear é dado por:

Para achar a solução particular do sistema linear, olhemos para a parte não homogênea .

Como ela só depende linearmente de t podemos supor que a solução particular é dada por:

Onde são constantes a serem determinadas.

Substituindo essa solução no nosso sistema linear, ficamos com:

Então temos que resolver o sistema abaixo:

Comparando o lado esquerdo com o lado direito, temos que ter

Resolvendo esse sisteminha achamos:

Portanto a solução particular do nosso sistema linear é:

Agora só somar a solução homogênea com a particular e temos:

c) Agora queremos achar a solução do sistema da letra (b) impondo a condição inicial

Bom, sabemos que a solução geral é dada por

Então,

Logo, fazendo as contas, achamos:

Então a solução do sistema com condição inicial é