Considere a matriz dada por
Determine os valores de de modo que no retrato de fase do sistema o ponto crítico seja um centro.
Para , encontre a solução do sistema e esboce o retrato de fase.
Passo 1
Nosso sistema é:
O sistema já está na forma matricial, então vamos resolver pelo método do cálculo funcional.
A primeira coisa que devemos fazer é identificar o valor da matriz
Passo 2
Agora temos que achar o autovalores de .
Lembra é só fazer
Como queremos que tenhamos o como centro estável, nosso precisa ser um imaginário puro. Então:
Passo 3
Bom, já vimos como são os nossos autovalores. Então, para , temos:
Como temos autovalores complexos o sistema para achar e vai ser
Com
Isso nos diz que
Com os nossos valores vai ficar
Esse é o momento que você para, respira fundo e pensa, agora ferrou!!!!! Quando a parada der complexa as contas vão ser levemente bizarras mesmo, mas relaxa que você consegue, me segue até o fim e não desiste.

Você deve estar pensando nesse maldito , relaxa, vamos fazer o temos feito, começar subtraindo a segunda equação da primeira
O valor de vai ser
Passo 4
A nossa solução vai ser
Substituindo os valores que temos
Passo 5
Supondo que a condição inicial seja
Então vamos ter
Passo 6
A solução vai ficar
Passo 7
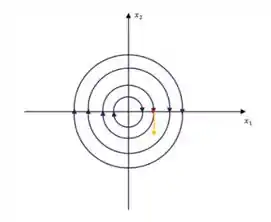
Agora só nos resta fazer o retrato de fase. Cara, a gente já viu na letra que para o retrato de fase é o centro estável. Então:
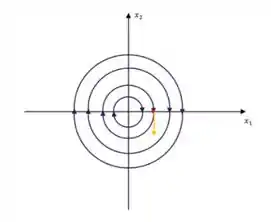
Resposta