Considere o átomo de hidrogênio no estado excitado, com um elétron no orbital 5p.
No diagrama abaixo, represente todas as transições de emissão possíveis para esse elétron, considerando apenas a série de Balmer. Calcule o comprimento de onda da radiação emitida de menor energia.
Passo 1
Fica calmo. Essa parada de 5p parece estranha mas, nesse momento, a única coisa que você tem que saber é que se o orbital é 5p, .
Como o enunciado deixa claro que só quer saber das transições que se enquadram na série de Balmer, a gente sabe que o do elétron é . Nesse caso, esse será o nível do elétron depois do salto (por se tratar de um espetro de emissão e ser o menor nível envolvido).
Aí a gente pode pensar que a única transição de emissão possível vai ser o elétron pulando de para . Mas isso não é verdade.
O elétron no nível 5 pode pular pro nível 2. Mas ele também pode pular pro nível 4 e depois ir pro nível 2 (em dois pulos sucessivos), ou pro nível 3 e depois ir por nível 2. E todos os pulos com vão aparecer no espectro como uma linha da série de Balmer, certo?
Passo 2
Então, a representação de todas as transições de emissão pertencentes à série de Balmer fica assim:
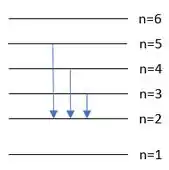
Passo 3
Pra calcular o comprimento de onda da radiação de menor energia a gente precisa, primeiro, decidir qual das transições envolve uma menor diferença de energia.
Eaí?
A transição que envolve menor diferença de energia é, justamente, a que envolve menor diferença entre os níveis.
Então: e .
Agora joga esses valores de na fórmula, substitui e calcula o .
Resposta