Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Singularidade

Ver Teoria
Exercício 111234567891012131415161718

Enunciado

Calcular ∫ C F → d r → , onde C é a curva parametrizada t → 3 s e n t , t , 2 cos ⁡ t , para t ∈ 0,2 π e

F → x , y , z = - z x 2 + z 2 + x , y , x x 2 + z 2 + z

Passo 1

Bom galera, algo que ajuda bastante a resolver esse problema é desenhar a curva para visualizar melhor o que está acontecendo. Analisando primeiramente um plano XZ, veremos de que se trata de uma elipse devido ao fato de termos nesses eixos seno e cosseno com constantes diferentes multiplicando-os. (Eixo X em vermelho e eixo Z em azul)

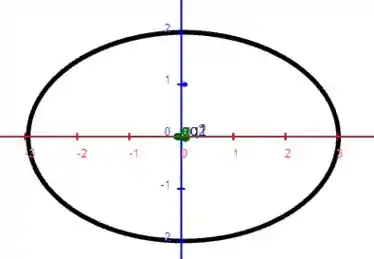
Porém o fato de ter no eixo Y, uma equação y = t , a medida que a elipse vai se formando, ela vai crescendo ao longo do eixo Y.

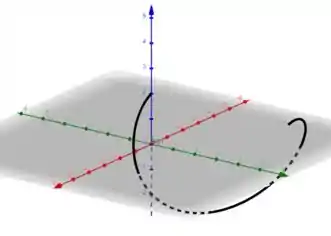
Passo 2

Resolver essa integral de linha normalmente é muito trabalhosa e utilizar Stokes é o indicado para essa questão. Porém para aplicar Stokes, temos algumas regrinhas:

  1. Ter uma curva fechada:

    2. Para isso iremos traçar uma curva Γ 1 que ligue as extremidades da curva do problema.

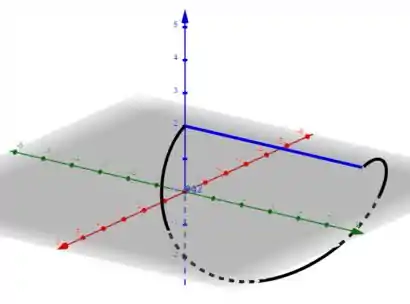
    Temos que ficar atentos ao sentido da curva!!!!!!!

    A curva do problema está orientada no sentido do eixo Y positivo, conforme mostram as setas pretas na imagem. Portanto a nova curva traçada precisará estar orientada no sentido Y negativo, o que garantirá a orientação correta dessa nova curva fechada.

    Essa nossa curva Γ 1 é parametrizada por:

    σ 1 → ( t ) :   0 , t , 2 ,   t   ∈ [ 0,2 π ]

    Na forma que tá aí, ela está com sentido contrário ao que a gente quer. Por isso depois quando formos calcular a integral de linha, iremos colocar ela com sinal negativo e assim respeitar o sentido que queremos.

  2. Não possuir singularidade:

A singularidade do nosso campo vetorial está ao longo de todo o eixo Y, pois x = z = 0 , então teremos no denominador x 2 + z 2 = 0 .

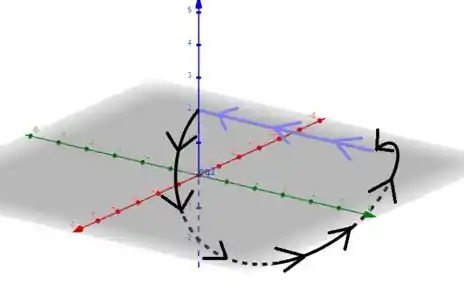
Para contornar esse problema iremos utilizar uma curva Γ 2 que segue o parâmetro:

σ 2 → ( t )   : 2 s e n t , 0,2 cos ⁡ t ,   t ∈ [ 0,2 π ]

A adição dessa curva irá possibilitar que a superfície considerada seja uma parte de um cilindro, contornando assim a singularidade.

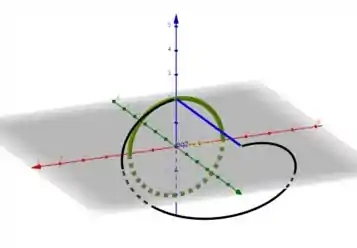
Não podemos esquecer da orientação, que pra esse caso deve ser a contrária da que está parametrizada, pois num cilindro as bases devem estar em sentidos contrários.

Passo 3

Agora é a hora das contas. Pelo teorema de Stokes:

∫ C F → d r → + ∫ Γ 1 - F → d r → + ∫ Γ 2 - F → d r →     = ∬ S r o t F d r →

Colocamos nas integrais Γ 1 - e   Γ 2 - pois foi necessário trocar o sentido das curvas.

Vamos começar calculando o rotacional de F :

r o t F = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3

F 1 = - z x 2 + z 2 + x

F 2 = y

F 3 = x x 2 + z 2 + z

r o t F = ( 0,0 , 0 )

Como o rotacional é nulo e já encontramos uma superfície que foge da singularidade, nossa integral de superfície será nula.

∬ S r o t F d r → = 0

Passo 4

Vamos calcular a integral de linha da curva Γ 1 - :

∫ Γ 1 - F → d r → =   - ∫ 0 2 π F ( 0 , t , 2 ) .   σ 1 → ' ( t ) d t

∫ Γ 1 - F → d r → = - ∫ 0 2 π - 2 0 2 + 2 2 + 0 , t , 0 0 2 + 2 2 + 2 . ( 0,1 , 0 ) d t

∫ Γ 1 - F → d r → = - ∫ 0 2 π t d t

∫ Γ 1 - F → d r → = - t 2 2 0 2 π = - 2 π 2

Passo 5

Agora partimos para nossa última integral

∫ Γ 2 - F → d r → =   - ∫ 0 2 π F 2 s e n t , 0,2 cos ⁡ t .   σ 2 → ' ( t ) d t

∫ Γ 2 - F → d r → = - ∫ 0 2 π - 2 cos ⁡ t ( 2 s e n t ) 2 + ( 2 cos ⁡ t ) 2 + 2 s e n t , 0 , 2 s e n t ( 2 s e n t ) 2 + ( 2 cos ⁡ t ) 2 + 2 cos ⁡ t . ( 2 c o s t , 0 , - 2 s e n t ) d t

∫ Γ 2 - F → d r → = - ∫ 0 2 π - cos 2 ⁡ t + 4 s e n t cos ⁡ t - s e n 2 t - 4 s e n t cos ⁡ t d t = - ∫ 0 2 π - d t

∫ Γ 2 - F → d r → = t 0 2 π = 2 π

Passo 6

Agora só precisamos substituir:

∫ C F → d r → + ∫ Γ 1 - F → d r → + ∫ Γ 2 - F → d r →     = ∬ S r o t F d r →

∫ C F → d r → - 2 π 2 + 2 π = 0

∫ C F → d r → = 2 π 2 - 2 π

Resposta

∫ C F → d r → = 2 π 2 - 2 π