Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Singularidade

Ver Teoria
Exercício 812345679101112131415161718

Enunciado

Seja γ a curva de interseção do cone z + 3 2 = y - 1 2 + x 2 com o plano z = 4 , orientada no sentido anti-horário quando vista de cima do eixo O z . Usando o teorema de Stokes, calcular ∫ γ   F →   d r → se

F → = 1 - y y - 1 2 + x 2 + y ,   x y - 1 2 + x 2 ,   x - 2 z sin ⁡ 1 + z 8 .

Passo 1

Como vamos utilizar o Teorema de Stokes para matar o nosso problema, eis a sua linda igualdade :

∫ γ   F →   d r → = ∬ S   r o t   F → ∙ n →   d S

A igualdade de uma integral de linha, com a integral de superfície do rotacional. Maaaas, não podemos sair aplicando essa igualdade assim, de qualquer maneira. Sempre temos que, antes de aplicar a igualdade, avaliar as condições de Stokes:

  1. Ter uma curva γ fechada e como borda de uma superfície S .
  2. Campo F → sem singularidades onde estamos trabalhando.
  3. Superfície S orientada positivamente em relação à curva.

Bora então verificar cada uma dessas condições para depois aplicar o nosso amado Stokes?

Passo 2

A primeira fala que temos que ter uma curva γ fechada, será que ela é? Vamos desenha-la:

Ela é a intercessão desse cone z + 3 2 = y - 1 2 + x 2 deslocado de 3 unidades para baixo em z e uma em y :

Com o plano z = 4 , formando essa espécie de circunferência no espaço aqui, oh:

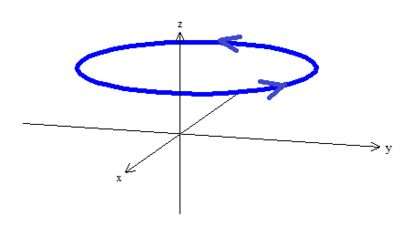
(lembre-se de coloca-la girando no sentido pedido )

Muito bem, a curva é fechada! Precisamos de uma superfície que a tenha como borda. Normalmente, pegaríamos esse próprio pedacinho de plano dentro dela:

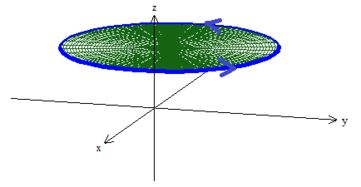
O problema dessa superfície é que ela fere a segunda condição do teorema: campo F → sem singularidades onde estamos trabalhando. Quer saber o porquê? Acompanhe-me, por gentileza !

Passo 3

Ora! Repare que o campo vetorial F → , tem um problema:

F → = 1 - y y - 1 2 + x 2 + y ,   x y - 1 2 + x 2 ,   x - 2 z sin ⁡ 1 + z 8

Quando fazemos y = 1 e x = 0 , esse cara do denominador, y - 1 2 + x 2 , zera! O que sabemos que não pode acontecer. Então todos os pontos que tem x = 0 e y = 1 , faz esse campo dar problema. Essa reta é justamente essa vermelha aqui, oh, paralela a z ...

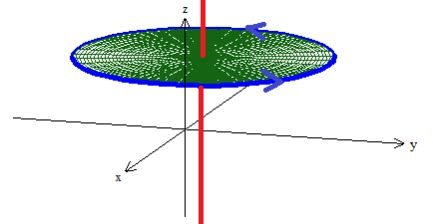
Note que essa reta, atravessa a superfície que tínhamos escolhido a priori, nos levando a... Não pegar esse plano verde como superfície, sacou?!

A superfície que vamos pegar então é justamente esse pedacinho de cone que vai do plano z = 0 até lá em cima:

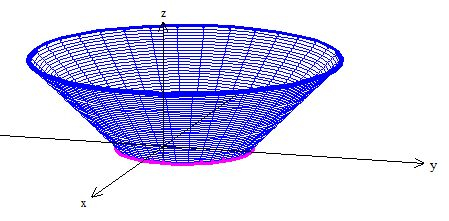
Repare que ele não tem a singularidade (a reta vermelha não o atravessa) e ele também tem a curva γ como uma borda! :D

Passo 4

Superfície escolhida, só falta mais uma coisa: orienta-la positivamente com a curva. Isso significa que temos que ver onde o vetor normal na superfície está apontando. Fazemos isso utilizando a regra da mão direita!

Observe que a curva está girando naquele sentido ali, certo? Então com a sua mão direita, você vai colocar os dedos na direção de giro dela e com o polegar pra cima, você vai ver o vetor normal. Veja!

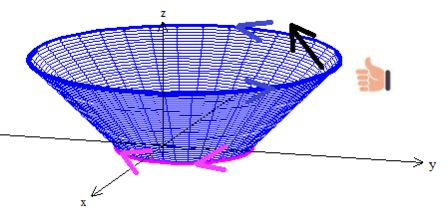
Viu só? O vetor normal no caso está “dentro” do cone.

Com isso, devemos orientar aquela curva lá em baixo que deve estar girando no sentido horário quando vista de cima para baixo, percebeu?

Passo 5

Beleza, condições satisfeitas, podemos aplicar o Teorema, ou melhor, a igualdade:

∫ ∂ S   F →   d r → = ∬ S   r o t   F → ∙ n →   d S

Repara que a integral de linha tem que ser calculada na borda ∂ S . E a borda é a junção da curva γ com aquela curva no plano z = 0 que podemos nomear de γ 2 . Sendo assim:

∫ γ   F →   d r → + ∫ γ 2   F →   d r → = ∬ S   r o t   F → ∙ n →   d S

Se queremos a integral de linha sobre a γ ...

∫ γ   F →   d r → = ∬ S   r o t   F → ∙ n →   d S - ∫ γ 2   F →   d r →

Temos então que calcular essas duas integrais aí!

Vamos começar pela majestosa integral de superfície. Para a resolução dela, seguimos o passo a passo de integrais de superfície:

  1. Parametrizar a superfície S pedida no problema.
  2. Encontrar o termo n → d S .
  3. Encontrar o r o t ( F → ).

Passo 6

Podemos parametrizar um pedacinho de cone normal ( z 2 = x 2 + y 2 ) com as primas das coordenadas cilíndricas:

x = r cos ⁡ θ

y = r sin ⁡ θ

Assim, substituindo na fórmula do cone, ganhamos:

z 2 = x 2 + y 2         →           z 2 = r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ     →

z 2 = r 2 cos 2 ⁡ θ + sin 2 ⁡ θ         →             z 2 = r 2         →

z = r

Porém, o nosso cone não tão normal assim, pois ele está descolado z + 3 2 = y - 1 2 + x 2 . Mas basta a gente fazer então, uma pequena mudança:

x = r cos ⁡ θ

y - 1 = r sin ⁡ θ

z + 3 = r

Logo, a nossa parametrização bonitinha é:

σ r ,   θ = r cos ⁡ θ ,   r sin ⁡ θ + 1 ,   r - 3

Sacou?

Passo 7

Nunca saímos de uma parametrização sem antes dizer onde os parâmetros estão variando, r e θ no caso.

Mas pow! r é z + 3 e como z varia do plano z = 0 até o plano z = 4 lá em cima...

0 + 3 ≤ r ≤ 4 + 3     →

3 ≤ r ≤ 7

Quanto ao ângulo θ , bem, se olharmos de cima pra baixo

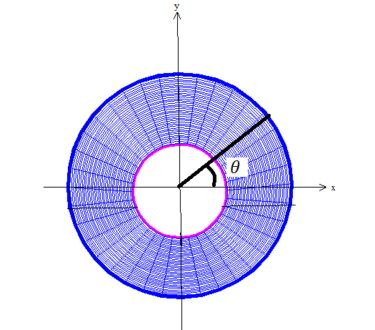
vamos percebebem que o θ tem que dar uma volta completa:

0 ≤ θ ≤ 2 π

Passo 8

Muito bem, parametrização dada como concluída, podemos buscar o termo n → d S :

n → d S = N →   d r d θ

Onde esse vetor norma N → ...

N → = ∂ σ ∂ r × ∂ σ ∂ θ

Como σ r ,   θ = r cos ⁡ θ ,   r sin ⁡ θ + 1 ,   r - 3 , podemos calcular essas derivadas parciais:

∂ σ ∂ r = cos ⁡ θ , sin ⁡ θ ,   1

∂ σ ∂ θ = - r sin ⁡ θ ,   r cos ⁡ θ ,   0

Um produto vetorial é dado pelo determinando dos vetores calculados...

N → = ∂ σ ∂ φ × ∂ σ ∂ θ

N → = i → j → k → cos ⁡ θ sin ⁡ θ 1 - r sin ⁡ θ r cos ⁡ θ 0

N → = - r sin ⁡ θ j → + r cos 2 ⁡ θ k → - r cos ⁡ θ i → - r sin 2 ⁡ θ k →

N → = - r cos ⁡ θ i → - r sin ⁡ θ j → + r cos 2 ⁡ θ k → + r sin 2 ⁡ θ k →

Colocando em evidência a parte do k → ...

N → = - r cos ⁡ θ i → - r sin ⁡ θ j → + r cos 2 ⁡ θ + sin 2 ⁡ θ k →

N → = - r cos ⁡ θ i → - r sin ⁡ θ j → + r   k →

Logo o vetor normal é...

N → = - r cos ⁡ θ ,   - r sin ⁡ θ ,   r

Como o Vetor normal que queremos tem a coordenada está pra cima ( z positivo) esse é justamente o vetor normal que vimos na regra da mão direita, saca? Se ele tiver com a terceira coordenada negativa, basta mudar o sinal das três entradas :)!

n → d S = - r cos ⁡ θ ,   - r sin ⁡ θ ,   r   d r d θ

Passo 9

Para encontrar o r o t F → , basta aplicar a fórmula do rotacional:

r o t F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Sendo

F → = 1 - y y - 1 2 + x 2 + y ,   x y - 1 2 + x 2 ,   x - 2 z sin ⁡ 1 + z 8 = F 1 ,   F 2 ,   F 3

Basta calcular cada uma dessas derivadas parciais aí e ser feliz:

1 º )                 ∂ F 3 ∂ y = ∂ x - 2 z sin ⁡ 1 + z 8 ∂ y = 0

2 º )                                 ∂ F 2 ∂ z = ∂ x y - 1 2 + x 2 ∂ z = 0

3 º )                   ∂ F 1 ∂ z = ∂ 1 - y y - 1 2 + x 2 + y ∂ z = 0

4 º )                   ∂ F 3 ∂ x = ∂ x - 2 z sin ⁡ 1 + z 8 ∂ x = 1

5 º )                                           ∂ F 2 ∂ x = ∂ x y - 1 2 + x 2 ∂ x =

Cuidado com a regra da fração nesse daí, heim:

y - 1 2 + x 2 - x ∂ y - 1 2 + x 2 ∂ x y - 1 2 + x 2 2 =

y - 1 2 + x 2 - 2 x 2 y - 1 2 + x 2 2 = y - 1 2 - x 2 y - 1 2 + x 2 2

Por fim, e também tomando cuidado com a regra da fração (vai dar um resultado muito parecido ):

6 º )                           ∂ F 1 ∂ y = ∂ 1 - y y - 1 2 + x 2 + y ∂ y =

- y - 1 2 + x 2 - 1 - y ∂ y - 1 2 + x 2 ∂ y y - 1 2 + x 2 2 + 1 =

- y - 1 2 + x 2 + 2 1 - y 2 y - 1 2 + x 2 2 = y - 1 2 - x 2 y - 1 2 + x 2 2 + 1

Voltando para o rotacional:

r o t F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

r o t F → = 0 - 0 ,   0 - 1 ,   y - 1 2 - x 2 y - 1 2 + x 2 2 - y - 1 2 - x 2 y - 1 2 + x 2 2 + 1

r o t F → = 0 ,   - 1 ,   - 1

Passo 10

Voltando para a integral de superfície

∬ S   r o t   F → ∙ n →   d S

Os substituindo os limites...

3 ≤ r ≤ 7

0 ≤ θ ≤ 2 π

O rotacional, e também substituindo o n →   d S

∬ S   r o t   F → ∙ n →   d S = ∫ 0 2 π ∫ 3 7 0 ,   - 1 ,   - 1 ∙ - r cos ⁡ θ ,   - r sin ⁡ θ ,   r   d r d θ =

∫ 0 2 π ∫ 3 7 r sin ⁡ θ - r   d r d θ =

∫ 0 2 π ∫ 3 7 r sin ⁡ θ - r   d r d θ =

∫ 0 2 π sin ⁡ θ r 2 2 - r 2 2 3 7 d θ =

∫ 0 2 π sin ⁡ θ 7 2 2 - 7 2 2 - sin ⁡ θ 3 2 2 - 3 2 2 d θ =

∫ 0 2 π 49 sin ⁡ θ - 1 2 - 9 sin ⁡ θ - 1 2 d θ =

∫ 0 2 π 40 sin ⁡ θ - 1 2 d θ =

20 ∫ 0 2 π sin ⁡ θ - 1   d θ =

20 - cos ⁡ θ - θ 0 2 π =

- 40 π

Passo 11

Calma que ainda não acabou. Temos que calcular essa integral de linha sobre essa curva γ 2 (circunferência no plano z = 0 ):

∫ γ 2   F →   d r →

E para calcula-la também vamos fazer do modo direto. Venha comigo

Passo 12

Primeiro, devemos parametrizar a curva.

Como é um círculo que pertence ao cone

z + 3 2 = y - 1 2 + x 2

mas tem z = 0 ...

9 = y - 1 2 + x 2

É uma circunferência de raio 3 deslocada em uma unidade em y . Então pode ser parametrizada como:

x = 3 cos ⁡ θ

y - 1 = 3 sin ⁡ θ

Como essa curva está no plano z = 0 ...

z = 0

Ou melhor...

δ θ = 3 cos ⁡ θ ,   3 sin ⁡ θ + 1 ,   0

Onde θ dá uma volta completa

0 ≤ θ ≤ 2 π

Agora precisamos do termo d r → ...

d r → = δ ' θ d θ

δ ' θ = - 3 sin ⁡ θ , 3 cos ⁡ θ ,   0

Passo 13

Substituindo os termos do campo pelos termos da parametrização...

F → = 1 - y y - 1 2 + x 2 + y ,   x y - 1 2 + x 2 ,   x - 2 z sin ⁡ 1 + z 8       →

Lembre-se que y - 1 2 + x 2 = 9 ...

F → = 1 - 3 sin ⁡ θ + 1 9 + 3 sin ⁡ θ + 1 ,   3 cos ⁡ θ 9 , 3 cos ⁡ θ       →

F → = - 1 3 sin ⁡ θ + 3 sin ⁡ θ + 1 , 1 3 cos ⁡ θ , 3 cos ⁡ θ    

Substituindo tudo na integral...

∫ γ 2   F →   d r → =

∫ 0 2 π - 1 3 sin ⁡ θ + 3 sin ⁡ θ + 1 , 1 3 cos ⁡ θ , 3 cos ⁡ θ   ∙ - 3 sin ⁡ θ , 3 cos ⁡ θ ,   0   d θ =

∫ 0 2 π sin 2 ⁡ θ - 9 sin 2 ⁡ θ - 3 sin ⁡ θ + cos 2 ⁡ θ   d θ =

∫ 0 2 π - 9 sin 2 ⁡ θ - 3 sin ⁡ θ + sin 2 ⁡ θ + cos 2 ⁡ θ   d θ =

∫ 0 2 π - 9 sin 2 ⁡ θ - 3 sin ⁡ θ + 1   d θ =

∫ 0 2 π - 9 sin 2 ⁡ θ d θ + ∫ 0 2 π - 3 sin ⁡ θ + 1   d θ =

Lembrando que sin 2 ⁡ θ = 1 - cos ⁡ 2 θ 2 ...

- 9 ∫ 0 2 π 1 - cos ⁡ 2 θ 2 d θ + 3 cos ⁡ θ + θ 0 2 π =

- 9 1 2 θ - sin ⁡ 2 θ 4 0 2 π + 3 cos ⁡ θ + θ 0 2 π =

- 9 1 2 2 π + 2 π =

- 7 π

Embora o resultado deu negativo, quero que perceba que com a parametrização que fizemos

δ θ = 3 cos ⁡ θ ,   3 sin ⁡ θ + 1 ,   0

A curva gira no sentido anti-horário se visualizarmos de cima para baixo:

Porém, vimos que para o conjunto superfície-borda estarem orientadas positivamente, precisamos dessa curva girando no sentido horário, por isso devemos inverter o sinal do resultado que encontramos ficando:

∫ γ 2   F →   d r → = 7 π

Passo 14

Finalmente retornando a igualdade do teorema:

∫ γ   F →   d r → = ∬ S   r o t   F → ∙ n →   d S - ∫ γ 2   F →   d r →

e substituindo ambos resultados...

∫ γ   F →   d r → = - 40 π - 7 π

∫ γ   F →   d r → = - 47 π

Resposta

- 47 π