Seja
Mostre que , onde é a curva , orientada no sentido anti-horário.
Passo 1
Vamos procurar alguma singularidade, olha a fração! Já vamos desconfiar que pode existir alguma coisa aí!
O demoninador da fração é , então vamos igualar ele a zero:
Para isso devemos ter
Então existe uma singularidade de eixo, eixo . Não podemos usar nenhuma superfície que tenha intercessão com o eixo .
Passo 2
A superfície mais fácil de calcular a integral de linha seria o círculo limitado por , mas esta superfície passa pelo ponto , que é um ponto de singularidade.
Então vamos pegar uma coroa circular limitada pelas curvas e . Agora vamos analisar as orientações, como está no sentido anti-horário, pela regra da mão direita a normal aponta para o sentido positivo de .
A nova curva, , para seguir a mesma orientação deve estar no sentido horário! Veja a figura:
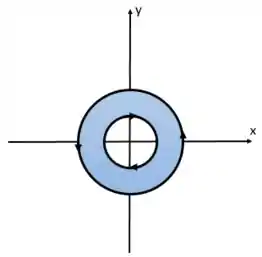
Passo 3
Aplicando o teorema de Stokes nesta superfície teremos:
Passo 4
Calcular o rotacional do campo,
Tempos,
Logo,
Passo 5
Calcular a integral de linha da curva ,
Parametrização de :
Assim,
Como ela está no sentido horário,
Passo 6
Por último vamos substituir os resultados dos passos 4 e 5 na equação resultante do teorema de Stokes!
Como foi pedido na questão!
Passo 7
Podemos resolver está integral pela definição de integral de linha! Veja,
Assim, o promeito passo é parametrizar a curva : e . Como é uma circunferência de raio igual a , pode ser parametrizada por:
Passo 8
Vamos calcular a integral,
Usando a relação fundamental da trigonometria ,
Resposta
Ei, a resposta está no passo a passo :)