Questão 4:
Sejam
e a intersecção do paraboloide com a esfera , orientada de forma que sua projeção no plano seja percorrida uma vez no sentido horário. Calcule .
Passo 1
Não sei você, mas eu estou sentindo cheiro de um Stokes aí, heim?! Por quê? Uai, nós temos um campo bizarro e uma curva igualmente bizarra (mesma se desenhar ela já me pareceu complexa). Mas se você quer ter certeza de que de fato estamos trabalhando com Stokes, calculemos o rotacional...
Como no nosso caso...
As primeiras derivadas já saem diretamente...
Essas duas últimas que vão dar um pouco de mais trabalho, afinal teremos que aplicar a regra da fração...
Calculando a outra de firma bem parecida
Logo...
Passo 2
O rotacional é muito easy, o que significa que de fato vamos aplicar o Teorema de Stokes:
Mas cuidado! Não podemos sair aplicando essa igualdade de qualquer forma. Precisamos antes averiguar as condições do Teorema.
O teorema de Stokes nos pede três coisas antes de aplicarmos a sua igualdade:
- Precisamos de uma curva fechada delimitando uma superfície .
- Outra exigência do teorema é que o campo , não tenha singularidades onde estamos trabalhando.
- A última, nos fala que a curva e a superfície devem estar orientadas positivamente.
Passo 3
Bem, de acordo com a condição acima, precisamos de uma curva fechada delimitando uma superfície . Mas por falar nisso, quem é essa curva? Ela é fechada e delimita alguma superfície?
Para responder essas perguntas, desenhemos no espaço de acordo com as orientações do enunciado:
Uma curva dado pela intersecção de um paraboloide com a “boca” pra cima e passando por , com uma esfera de raio ...
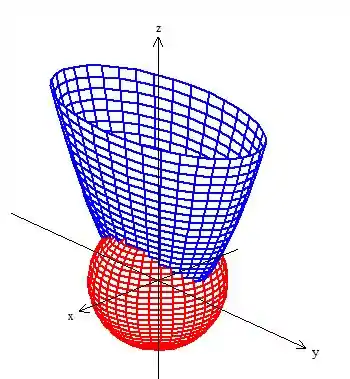
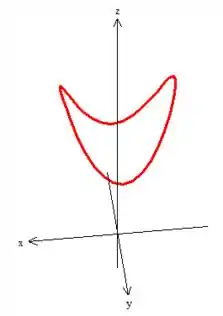
Eis a curva!
E repara que existem várias superfícies que ela delimita, entre elas, podemos pegar o próprio pedaço de paraboloide:
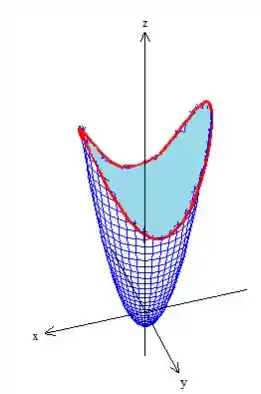
Passo 4
Outra condição nos pede um campo sem singularidades onde estamos trabalhando. O campo ...
Até tem uma singularidade em toda reta , pois se você substituir e em sua equação, ganharemos uma divisão por o que já sabemos ser impossível.
Então, não podemos usar todo o paraboloide
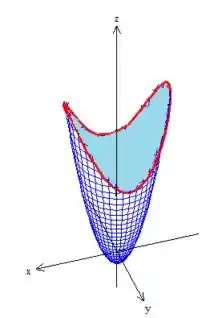
Pois ele passa pela singularidade. Mas calma que resolver esse problema é fácil, basta tirarmos o pedacinho de baixo, como se cortássemos pelo plano ...
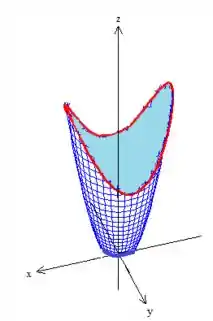
Eis a nossa superfície que vamos usar! :D
Passo 5
A última condição nos fala sobre a orientação ser positiva. Cara, isso significa que as curvas e a superfície devem estar orientadas juntas. Veja bem:
De acordo com o enunciado, temos que a curva lá em cima, se projetássemos no plano , a veríamos girando no sentido horário. Isso significa que ela, a própria , gira nesse sentido se olhássemos de cima para baixo:
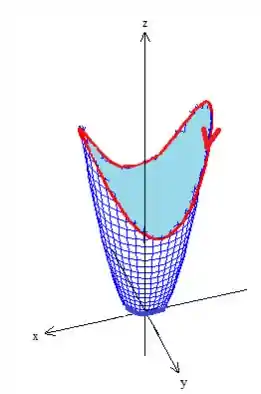
Pela regra da mão direita, colocando os dedos na direção de giro dela, descobrimos que o vetor normal à superfície deve estar saindo.
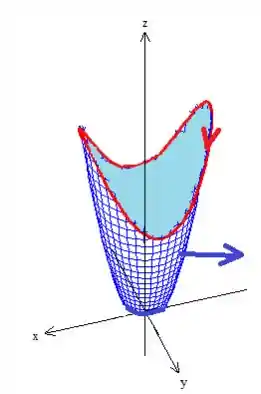
Assim, conseguimos determinar o sentido de giro daquela curvinha lá em baixo que vamos nomear de pela própria regra da mão direita...
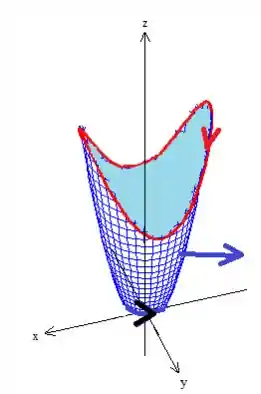
Prontinho! Orientada positivamente, sacou? ;)
Passo 6
Condições do teorema sendo satisfeitas, podemos aplicar a igualdade de Stokes...
Veja bem que na integral de linha, colocamos um representando que a integral de linha deve ser calculada na borda de . A borda, no caso, é a junção da curva com a ...
Como o rotacional j�� calculado foi nulo, a integral tripla desaparece...
Se queremos a integral de linha em cima de ...
Passo 7
Vamos calcular então essa integral de linha em cima de ...
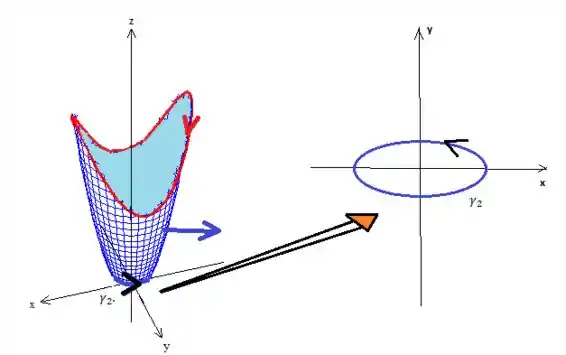
Primeiro, precisamos parametriza-la. Essa curva pode ser obtida fazendo a intersecção do paraboloide com o plano ...
Como desconfiávamos... Uma elipse. Podemos parametriza-la fazendo
E
Onde ...
Passo 8
Precisamos agora determinar o campo nas novas coordenas...
Como ...
Passo 9
Calculemos agora o termo ...
Jogando tudo na integral de linha que queremos resolver...
De acordo coma igualdade de Stokes que vimos...