Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Singularidade

Ver Teoria
Exercício 121234567891011131415161718

Enunciado

Questão 4: Utilize o teorema de Stokes para calcular

∫ C   F ⋅ d r →

Onde

F x ,   y ,   z = - y x 2 + y 2 , x x 2 + y 2 ,   x

E C é a intersecção do cilindro x 2 + y 2 = 1 com o plano z - y = 1 orientada de modo que a projeção no plano x y é percorrida no sentido anti-horário.

Passo 1

O problema já nos pediu para resolver o a integral de linha acima usando Stokes, só que se ele não nos tivesse pedido, teria como de saber que usando Stokes o problema sai muuuuito mais fácil que se tentarmos resolver a integral de linha na mão. O jeito é calculando o Rotacional:

r o t   F = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Onde F 1 , F 2 e F 3 são as componentes do campo F ...

F = F 1 ,   F 2 ,   F 3 = - y x 2 + y 2 , x x 2 + y 2 ,   x

De todas aquelas derivadas parciais ali em cima, as que vão dar certo trabalho são as duas últimas, pois vai ter que aplicar a regra da fração:

∂ F 2 ∂ x = ∂ ∂ x x x 2 + y 2 = x 2 + y 2 ⋅ ∂ ∂ x x - x ⋅ ∂ ∂ x x 2 + y 2 x 2 + y 2 2 =

x 2 + y 2 - x ⋅ 2 x x 2 + y 2 2 = - x 2 + y 2 x 2 + y 2 2

Para a outra derivada chata...

∂ F 1 ∂ y = ∂ ∂ y - y x 2 + y 2 = x 2 + y 2 ⋅ ∂ ∂ x - y - - y ⋅ ∂ ∂ x x 2 + y 2 x 2 + y 2 2 =

- x 2 + y 2 + y ⋅ 2 y x 2 + y 2 2 = - x 2 + y 2 x 2 + y 2 2

Logo, calculando as outras derivadas que são bem tranquilas e substituindo no rotacional...

r o t   F = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y       →

r o t   F = ∂ x ∂ y - ∂ x x 2 + y 2 ∂ z ,   ∂ - y x 2 + y 2 ∂ z - ∂ x ∂ x ,   - x 2 + y 2 x 2 + y 2 2 - - x 2 + y 2 x 2 + y 2 2     →

r o t   F = 0 - 0 ,   0 - 1 ,   0   →

r o t   F = 0 ,   - 1 ,   0

E prontinho! Esse é o Rotacional! Veja como ele é beeeem mais simples que o próprio campo F x ,   y ,   z , sugerindo o Teorema de Stokes que mesmo que o problema não nos mandasse fazer por Stokes, sacou?

Passo 2

O Teorema de Stokes é a maravilhosa igualdade entre uma integral de linha e uma integral de superfície:

∫ C   F ⋅ d r → = ∬ S   r o t   F ⋅ n →   d S

Mas calma lá, jovem! Antes de aplicarmos o teorema em si, devemos verificar se estamos nas condições que o Teorema nos exige:

  1. Ter uma curva C fechada delimitando a superfície S .
  2. Um campo sem singularidades.
  3. E por último, ter uma orientação positiva.

Nos próximos três passos, vamos avaliar cada um deles, ok?

Passo 3

A primeira condição exige uma superfície fechada. Vamos ver se isso é verdade no enunciado:

“... C é a intersecção do cilindro x 2 + y 2 = 1 com o plano z - y = 1 ...”.

Bem, aqui não tem muito mistério, bastam desenhar as duas superfícies juntas e a curva vai aparecer na intersecção:

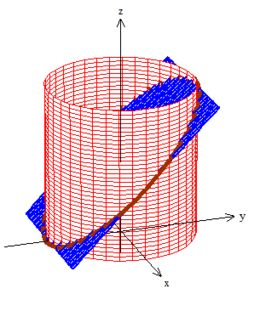
Viu só? Essa é benedita !

AHHH! Só mais um detalhe, temos que escolher uma superfície S que essa curva delimite! Pode ser qualquer superfície, então a um primeiro momento, vamos escolher o pedacinho de círculo em cima do plano z - y = 1 :

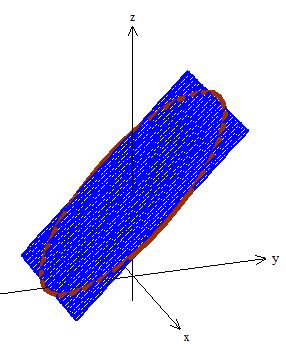
Passo 4

OLHA A PEGADINHO DO MALANDRO!!!

Vou te mostrar aqui o porquê daquela escolha de superfície ali em cima é uma escolha PROIBIDA! Sim, ela é uma escolha proibidíssima e o motivo é que essa superfície passa pela singularidade de F . Veja bem:

F x ,   y ,   z = - y x 2 + y 2 , x x 2 + y 2 ,   x

Analisando esse campo aí, a gente logo percebe que x e y não podem ser simultaneamente 0 . Isso porquê se não o denominador 0 o que não acontece, neh? Então, todos os pontos que isso acontece, são chamados de pontos de singularidade, e são pontos onde a função não existe! São esses pontos pintadinhos de amarelo aqui oh:

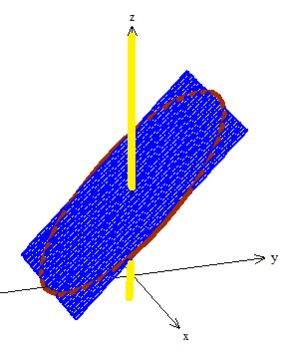
Percebeu? Então podemos escolher aquela superfície S . Qual outra superfície poderíamos escolher que tenha como borda aquela curva? Ora, se pegamos o plano e não funcionou, vamos pegar agora a superfície em cima do cilindro:

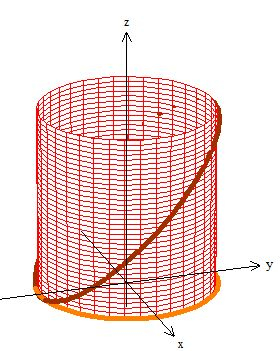
Essa superfície tem duas bordas ∂ S , uma é a curva C (que queremos), e a outra é a circunferência no chão (plano x y ), saca? A essa curva danemos um nome de C 1 . Isso que acabamos de falar em matemática é:

∂ S = C ∪ C 1

Passo 5

Finalmente, agora sem mais pegadinha e prosseguindo com essa superfície, devemos orienta-la positivamente. O problema disse que a curva C está girando de tal forma que a sua projeção no plano x y (sua sombra) gira no sentido anti-horário:

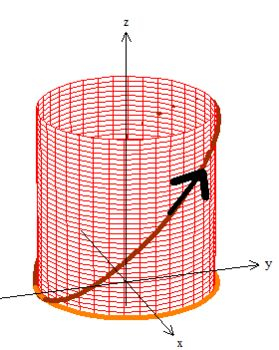
Pela regar da mão direita, então vemos que o vetor normal a esse cilindro está apontado para dentro, e isso faz com que a outra borda de S (a curva no chão) gire no sentido horário:

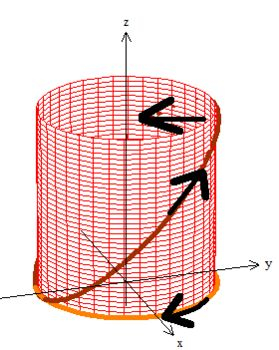
Passo 6

Com tudo isso sendo satisfeito, podemos finalmente retornar ao problema e aplicar S t o k e s sem medo de ser feliz:

∫ ∂ S   F ⋅ d r → = ∬ S   r o t   F ⋅ n →   d S

Como ∂ S = C ∪ C 1 ...

∫ C   F ⋅ d r → + ∫ C 1   F ⋅ d r → = ∬ S   r o t   F ⋅ n →   d S

Como queremos o resultado da integral em cima de C (curva da intersecção)...

∫ C   F ⋅ d r → = ∬ S   r o t   F ⋅ n →   d S - ∫ C 1   F ⋅ d r →

É só calcular essas duas integrais do lado direito e matar o problema!

Passo 7

Começando pela integral de superfície em cima do cilindro S ...

∬ S   r o t   F ⋅ n →   d S

  • Parametrizando a superfície, por ser um cilindro de raio 1 ... Podemos comparar com a mudança para coordenada cilíndrica (só que trocando o raio por 1 ):

    • x = 1 ⋅ cos ⁡ t

    y = 1 ⋅ sin ⁡ t

    z = z

    Então, a parametrização final fica:

    σ t ,   z = cos ⁡ t , sin ⁡ t ,   z

    Bem, t tem que dar uma volta completa:

    0 ≤ t ≤ 2 π

    Enquanto z varia do chão, até a curva C (encontro com o plano)

    0 ≤ z ≤ P l a n o   →

    0 ≤ z ≤ 1 + y   →

    0 ≤ z ≤ 1 + sin ⁡ t

  • Para o termo n →   d S ...

    • n → d S = N →   d z d t

    Onde

    N → = ∂ σ ∂ t × ∂ σ ∂ z

    Calculando essas derivadas parciais e jogando na fórmula de produto vetorial...

    i ^ j ^ k ^ - sin ⁡ t cos ⁡ t 0 0 0 1 =

    cos ⁡ t i ^ + sin ⁡ t j ^

    Ou seja:

    n → d S = cos ⁡ t , sin ⁡ t , 0   d z d t

    Agora cuidado! Porquê com esse vetor normal, estamos falando de um que está apontando para fora, e não é esse que queremos, neh? Então invertemos o seu sinal:

    n → d S = - cos ⁡ t , - sin ⁡ t , 0   d z d t

  • O rotacional também deve ser substituído pelos termos da parametrização.

    • F = 0 ,   - 1 ,   0     →

    F σ t ,   z = 0 ,   - 1 ,   0

    Agora é só substituir e matar a integral de superfície:

    ∬ S   r o t   F ⋅ n →   d S = ∫ 0 2 π ∫ 0 1 + sin ⁡ t 0 ,   - 1 ,   0 ⋅ - cos ⁡ t , - sin ⁡ t , 0   d z d t =

    ∫ 0 2 π ∫ 0 1 + sin ⁡ t sin ⁡ t   d z d t = ∫ 0 2 π sin ⁡ t + sin 2 ⁡ t d t =

    ∫ 0 2 π sin ⁡ t d t + ∫ 0 2 π sin 2 ⁡ t d t

    A primeira integral dá zero né? Estamos integrando seno no seu período. Então:

    ∬ S   r o t   F ⋅ n →   d S = ∫ 0 2 π sin 2 ⁡ t d t

    sin 2 ⁡ t costuma poder ser escrito como 1 - cos ⁡ 2 t 2 , então

    ∬ S   r o t   F ⋅ n →   d S = ∫ 0 2 π 1 - cos ⁡ 2 t 2 d t = t 2 - sin ⁡ 2 t 4 0 2 π = 2 π 2 - sin ⁡ 4 π 4 + sin ⁡ 0 4 =

    π

    Opa, show de bola,

    ∬ S   r o t   F ⋅ n →   d S = π

    Passo 8

    Agora só nos falta a integral de linha:

    ∫ C 1   F ⋅ d r →

  • Primeiro vamos parametrizar a curva C 1 (circunferência que está no chão):

    • x = cos ⁡ θ

    y = sin ⁡ θ

    z = 0

    Então

    r → θ = cos ⁡ θ , sin ⁡ θ ,   0

    0 ≤ θ ≤ 2 π

  • O termo d r → ...

    • d r → = r → ' θ d θ

    d r → = - sin ⁡ θ , cos ⁡ θ ,   0 d θ

    Só tem um problema, a curva no chão deve estar girando no sentido horário, e com esse d r → , ele está no sentido anti-horário (isso sempre acontece para essa parametrização padrão), então a gente inverte o sinal:

    d r → = sin ⁡ θ , - cos ⁡ θ ,   0 d θ

  • Substituindo os termos do campo F ...

F x ,   y ,   z = - y x 2 + y 2 , x x 2 + y 2 ,   x     →

Como x 2 + y 2 = 1 (raio do cilindro onde acurva está)

F r → θ = - sin ⁡ θ 1 , cos ⁡ θ 1 , cos ⁡ θ   →

F r → θ = - sin ⁡ θ , cos ⁡ θ , cos ⁡ θ

Substituindo...

∫ C 1   F ⋅ d r → = ∫ 0 2 π - sin ⁡ θ , cos ⁡ θ , cos ⁡ θ ⋅ sin ⁡ θ , - cos ⁡ θ ,   0 d θ =

∫ 0 2 π - sin 2 ⁡ θ - cos 2 ⁡ θ d θ = - ∫ 0 2 π sin 2 ⁡ θ + cos 2 ⁡ θ d θ =

- ∫ 0 2 π d θ =

- 2 π

Passo 8

Agora é só mesmo voltar para a integral que agente realmente quer encontrar:

∫ C   F ⋅ d r → = ∬ S   r o t   F ⋅ n →   d S - ∫ C 1   F ⋅ d r →     →

∫ C   F ⋅ d r → = π - - 2 π =

3 π

Resposta

3 π