Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Singularidade

Ver Teoria
Exercício 131234567891011121415161718

Enunciado

Questão 4: Calcule

∫ γ   F → ⋅ d r →

Onde

F → x ,   y ,   z = - y - 1 x 2 + y - 1 2 + z , x x 2 + y - 1 2 , e z 3

E γ é a intersecção da superfície z = y - 1 2 e x 2 + y - 1 2 = 1 orientada de projeção no plano x y é percorrida no sentido horário.

Passo 1

Bem a nossa primeira tarefa ao se deparar com um problema desses é de fato entender um pouco a questão. Nós estamos buscando a solução de uma integral de linha de um campo vetorial. Sempre podemos resolvê-la de pelo menos duas formas:

  1. Forma direta.
  2. Teorema de Stokes.

Perceba que o campo é muito feio para pensarmos em fazê-la pela forma direta, por isso podemos pensar na forma alternativa... O TEOREMA DE STOKES:

∫ ∂ S   F → ⋅ d r → = ∬ S   r o t F → d S →    

Passo 2

Mas assim... Ver o campo, falar que ele é “feio” não é o suficiente para falarmos que o teorema resolve o nosso problema sem grandes problemas. Para você ter certeza disso, te sugerimos que calcule primeiro aquele rotacional ali. Se ele for algo mais simples, então de fato o Teorema de Stokes resolve o problema de maneira “simples” (ou pelo menos de forma mais simples que os demais rsrs). Então vamos nessa:

r o t F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y →

Lembrando que F 1 , F 2 e   F 3 são componentes do campo...

F → x ,   y ,   z = F 1 ,   F 2 ,   F 3 = - y - 1 x 2 + y - 1 2 + z , x x 2 + y - 1 2 , e z 3

Podemos então calcular essas derivadas parciais...

r o t F → = 0 - 0 ,   1 - 0 ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Perceba que deixamos essas duas últimas, afinal elas vão dar um certo trabalhinho (tem que aplicar a regra do quociente):

∂ F 2 ∂ x = ∂ ∂ x x x 2 + y - 1 2 = x 2 + y - 1 2 ⋅ ∂ ∂ x x - x ⋅ ∂ ∂ x x 2 + y - 1 2 x 2 + y - 1 2 2 =

x 2 + y - 1 2 - x ⋅ 2 x x 2 + y - 1 2 2 =

- x 2 + y - 1 2 x 2 + y - 1 2 2

Calculando a outra derivada parcial chatinha...

∂ F 1 ∂ y = ∂ ∂ y - y - 1 x 2 + y - 1 2 + z =

x 2 + y - 1 2 ⋅ ∂ ∂ y - y - 1 - - y - 1 ⋅ ∂ ∂ y x 2 + y - 1 2 x 2 + y - 1 2 2 =

x 2 + y - 1 2 ⋅ - 1 + y - 1 ⋅ 2 y - 1 x 2 + y - 1 2 2 =

- x 2 - y - 1 2 + 2 y - 1 2 x 2 + y - 1 2 2 =

- x 2 + y - 1 2 x 2 + y - 1 2 2

Juntando tudo...

r o t F → = 0 ,   1 ,   - x 2 + y - 1 2 x 2 + y - 1 2 2 - - x 2 + y - 1 2 x 2 + y - 1 2 2   →

r o t F → = 0 ,   1 ,   0

Perceba que de fato o rotacional é um cara muito bonito! Essa é a sugestão máxima que de que pode resolver sem medo por Stokes que ele vai nos ajudar. Bora lá?

Passo 3

Como vimos, o teorema de Stokes é essa igualdade aqui:

∫ ∂ S   F → ⋅ d r → = ∬ S   r o t F → d S →    

Porém existem alguns detalhes que na verdade são condições de aplicação do teorema:

  1. Precisamos de uma curva fechada ∂ S delimitando uma superfície.
  2. Precisamos de um campo sem singularidades onde estamos trabalhando.
  3. Por fim, precisamos de uma orientação positiva.

Vamos avaliar condição por condição!

Passo 4

a )

A primeira condição trata-se de ter uma curva fechada. Então surge aí a primeira pergunta: será que estamos de fato trabalhando com uma curva γ fechada? Pelo enunciado...

“E γ é a intersecção da superfície z = y - 1 2 e x 2 + y - 1 2 = 1 ...”.

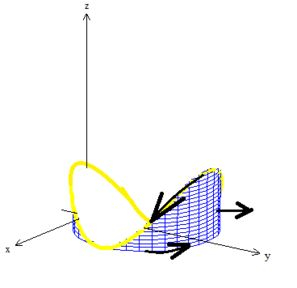
Desenhando essas superfícies:

A primeira é uma parábola com concavidade pra cima no plano z y . E no espaço ela translada em x já que a equação independe de x :

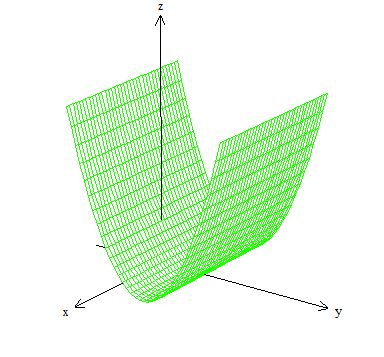
A segunda equação é um cilindro de raio 1 centrado em 0 ,   1 no plano x y ...

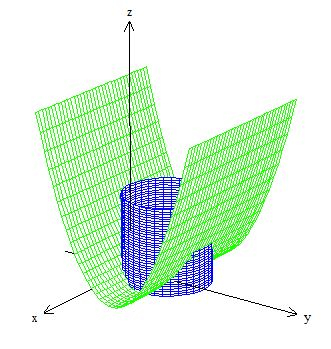
Veja a intersecção das duas superfícies ali formando a curva γ :

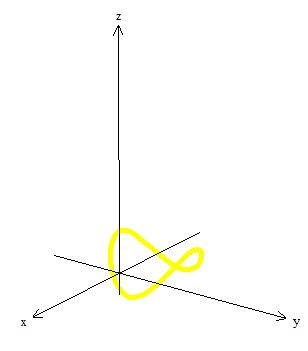
Que por sinal é fechada!

Passo 5

b )

Agora temos que escolher uma superfície que tenha como borda essa curva aí.

Poderíamos de imediato, pensar na superfície dessa superfície parabólica aí, já que ela é uma superfície simples que tem como bordo a curva γ (essa batata chips aqui):

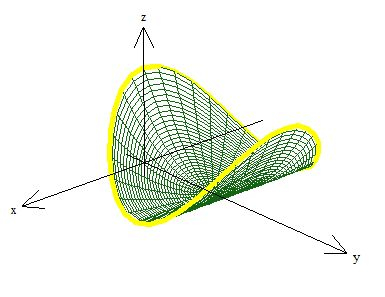
O GRANDE PROBLEMA dessa superfície é que ela fura outra condição:

  1. Precisamos de um campo sem singularidades onde estamos trabalhando.

Afinal, se olharmos para o campo F → com olhares mais atento...

F → x ,   y ,   z = - y - 1 x 2 + y - 1 2 + z , x x 2 + y - 1 2 , e z 3

Vamos perceber que o x e o y tem que ser diferente do ponto 0 ,   1 , afinal se isso acontecer ganhamos uma indeterminação... Uma singularidade.

O problema de escolher essa “batata chips” como superfície é justamente que ela contém esse ponto:

z = y - 1 2             →                 0 ,   1 ,   0           ( p o n t o   p e r t e n c e n t e   à   s u p e r f í c i e )

ORA! Se essa superfície não funcionou. Então pegamos a outra, ou seja, o cilindro: x 2 + y - 1 2 = 1 :

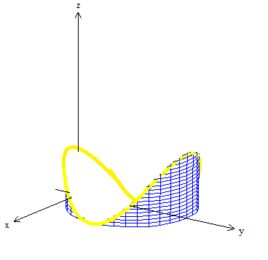
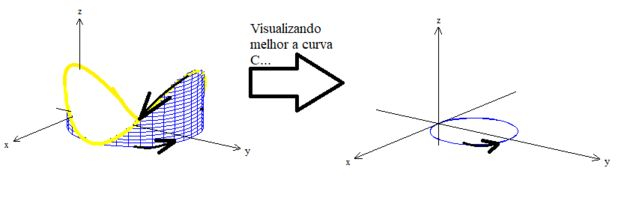
Vamos pegar ele indo de z = 0 até a curva γ (inclusive veja que em z = 0 ele tem outra borda que vamos chamar de C , ok?).

Passo 6

c )

A terceira e última análise diz respeito com a orientação disso tudo.

Pelo Teorema, temos que ter uma orientação positiva, o que significa que todas as curvas e superfície tem que estar de acordo com a regra da mão direita. Ou seja, sabemos que a curva γ gira no sentido horário:

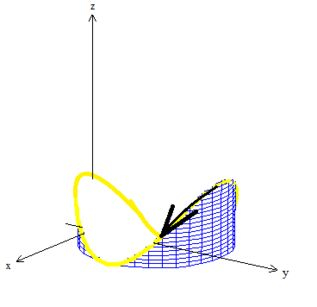
Então pela regra da mão direita, com os dedos no sentido de giro da curva e o dedão apontando pra fora, o vetor normal na superfície tem que estar saindo...

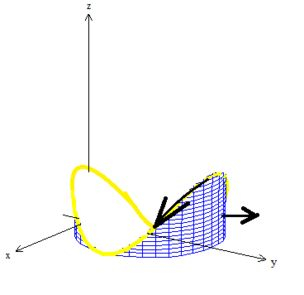
Com o vetor saindo, se aplicarmos novamente a regra da mão direita lá em baixo, vamos ver que a curva C que apareceu na história, a intrusa , gira no sentido anti-horário...

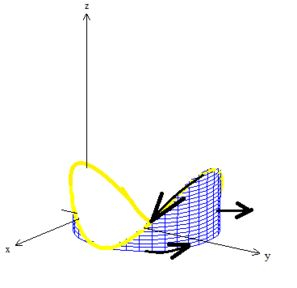
Prontinho! Agora todas estão orientadas positivamente!

Passo 7

Todas as condições averiguadas, podemos retornar para o teorema de Stokes:

∫ ∂ S   F → ⋅ d r → = ∬ S   r o t F → d S →     →

Perceba que agora a superfície S tem duas bordas ∂ S (Uma γ e outra C ):

∫ γ   F → ⋅ d r → + ∫ C   F → ⋅ d r → = ∬ S   r o t F → d S →     →

Como queremos a integral de linha em cima de γ , vamos isola-la...

∫ γ   F → ⋅ d r → = ∬ S   r o t F → d S → - ∫ C   F → ⋅ d r →  

Agora é só calcular essas integrais auxiliares aí e corrermos para o abraço! Eu sei... Parece loucura o que estamos fazendo. Trocando a solução de uma por duas integrais. Mas vai por mim... É bem mais fácil e rápido fazermos assim .

Passo 8

Vamos começar pela a solução da integral de superfície:

∬ S   r o t F → d S →

Como estamos trabalhando com um cilindro deslocado em y e com raio 1 , vamos usar a parametrização em coordenadas cilíndricas deslocadas...

x = 1 ⋅ cos ⁡ θ

y = 1 ⋅ sin ⁡ θ + 1

z = z   ( é   u m   p a r â m e t r o   q u e   n ã o   m u d a … C o n t i n u a   o   z   n o r m a l )

Ou... De uma forma mais bonita, a nossa parametrização em termos de θ e z é...

σ   θ ,   z = cos ⁡ θ ,   sin ⁡ θ + 1 ,   z

Para as variações dos parâmetros... O θ dá uma volta completa ao redor do centro do cilindro:

0 ≤ θ ≤ 2 π

Enquanto ao z varia do z de entrada ( z = 0 ), até a curva γ amarela...

0 ≤ z ≤ C u r v a   γ   →

A curva γ está delimitada pela parábola z = y - 1 2 :

0 ≤ z ≤ y - 1 2 ��     →

Colocando nas novas mudanças...

0 ≤ z ≤ sin 2 ⁡ θ

Passo 9

Para encontrar o termo d S → antes de voltarmos para a integral, apliquemos a teoria:

d S → = N →   d θ d z

Onde...

N → = ∂ σ ∂ θ × ∂ σ ∂ z

Calculando essas derivadas parciais:

σ   θ ,   z = cos ⁡ θ ,   sin ⁡ θ + 1 ,   z               →                   ∂ σ ∂ θ = - sin ⁡ θ , cos ⁡ θ ,   0

σ   θ ,   z = cos ⁡ θ ,   sin ⁡ θ + 1 ,   z               →                   ∂ σ ∂ z = 0,0 ,   1                                        

E lembrando que produto vetorial é um determinante:

N → = ∂ σ ∂ θ × ∂ σ ∂ z = i ^ j ^ k ^ - sin ⁡ θ cos ⁡ θ 0 0 0 1 =

cos ⁡ θ i ^ + sin ⁡ θ j ^

Chegamos a esse vetor normal:

N → = cos ⁡ θ , sin ⁡ θ ,   0

E repara que esse vetor normal atende a condição de estar para fora do cilindro, já que coordenadas estão positivas. Logo...

d S → = cos ⁡ θ , sin ⁡ θ ,   0   d θ d z

Passo 10

Voltando para a integral de superfície e substituindo tudo...

∬ S   r o t F → d S → = ∫ 0 2 π ∫ 0 sin 2 ⁡ θ 0 ,   1 ,   0 ⋅ cos ⁡ θ , sin ⁡ θ ,   0   d z d θ     →

Vamos encontra a seguinte integral dupla:

∫ 0 2 π ∫ 0 sin 2 ⁡ θ -   d z d θ

Calculando começando pela integral de dentro...

∫ 0 2 π sin ⁡ θ ∫ 0 sin 2 ⁡ θ   d z d θ

∫ 0 2 π sin ⁡ θ sin 2 ⁡ θ d θ = ∫ 0 2 π sin ⁡ θ 1 - cos 2 ⁡ θ d θ =

- ∫ 0 2 π sin ⁡ θ cos 2 ⁡ θ d θ + ∫ 0 2 π sin ⁡ θ d θ = cos 3 ⁡ θ 3 - cos ⁡ θ 0 2 π =

cos 3 ⁡ 2 π 3 - cos ⁡ 2 π - cos 3 ⁡ 0 3 - cos ⁡ 0 =

1 3 - 1 - 1 3 - 1 = 0

Passo 11

CALMA JOVEM! Ainda não acabamos! Falta ainda determinar essa integral de linha que apareceu (em cima da curva intrusa C )

∫ C   F → ⋅ d r →

Parametrizando C , lembrando que ela está em cima do cilindro de raio 1 e em cima de z = 0 ...

r → t = cos ⁡ t , sin ⁡ t + 1 ,   0

Com t dando uma volta completa para formar a circunferência:

0 ≤ t ≤ 2 π

Passo 12

Para encontrar o termo d r → , basta fazer:

d r → = r → ' t d t           →

d r → = - sin ⁡ t , cos ⁡ t ,   0 d t  

Passo 13

Então, antes de voltarmos para a integral de linha, devemos trocar os termos do campo, pelos termos da parametrização, lembrando que x 2 + y - 1 2 = 1 :

F → x ,   y ,   z = - y - 1 x 2 + y - 1 2 + z , x x 2 + y - 1 2 , e z 3   →

F → x ,   y ,   z = - y - 1 1 + z , x 1 , e z 3   →

Trocando x por cos ⁡ t , y = sin ⁡ t + 1 e z = 0 ...

F → r → t = - sin ⁡ t + 0 , cos ⁡ t , e 0 3   →

F → r → t = - sin ��� t , cos ⁡ t , 1

Passo 14

Voltando para a integral de linha em cima da intrusa...

∫ C   F → ⋅ d r → = ∫ 0 2 π - sin ⁡ t , cos ⁡ t , 1 ⋅ - sin ⁡ t , cos ⁡ t ,   0 d t =

∫ 0 2 π sin 2 ⁡ θ + cos 2 ⁡ θ d t = ∫ 0 2 π 1 d t =

2 π

Passo 15

VOCÊ ESTÁ REALMENTE APRESSADO, HEIM JOVEM? Calma! Ainda falta mais uma coisa... Voltar para o problema inicial (nos pedia o resultado da integral em cima de γ ):

∫ γ   F → ⋅ d r → = ∬ S   r o t F → d S → - ∫ C   F → ⋅ d r →   →

∫ γ   F → ⋅ d r → = 0 - 2 π   →

∫ γ   F → ⋅ d r → = - 2 π

Resposta

- 2 π