(7) Seja e a curva definida como a intersecção do cilindro com o plano . Para calcular , usando o teorema de Stokes, podemos considerar a seguinte superfície:
- A parte lateral do cilindro , onde
- O disco no plano
- A parte do paraboloide , onde
- A parte da esfera , onde
- A parte da esfera , onde
Passo 1
Bem, primeiro desenhemos a curva e como o próprio enunciado nos afirmou, ela é a intercessão do cilindro em torno de , ...
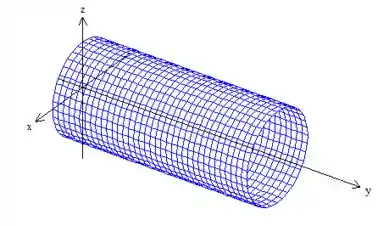
Com o plano fazendo uma secção nesse cilindro:
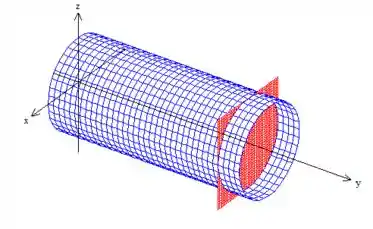
E a curva é justamente essa circunferência da secção:
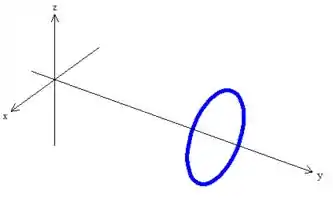
Viu só? :D
Passo 2
Bem, usualmente pegaríamos esse disco em cima do plano ...
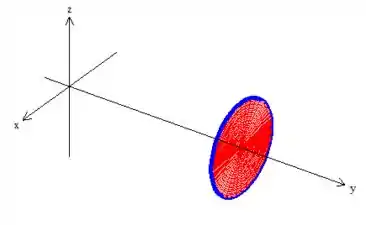
por ser mais simples, e marcaríamos o item . Massss, tem uma pegadinha aí!
Se você olhar atentamente para o campo
vai notar uma coisa: se substituíssemos ali e , ganharíamos uma divisão por o que sabemos ser impossível.
Logo, em todos os pontos que isso acontece (ao longo do eixo representado em verde abaixo) dizemos que o campo tem uma singularidade e isso não pode acontecer para aplicar Stokes!
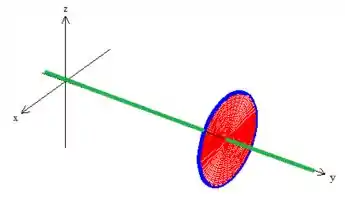
Então não podemos pegar esse disco, pois ele corta a singularidade, saca?
Passo 3
Mas não se preocupe, pois não podemos passar pela singularidade, mas podemos dar a volta nele, por isso deveríamos escolher o próprio cilindro azul
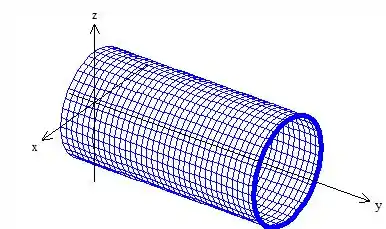
indo de até a curva que queremos, tornando a letra , a verdadeira!
Os demais itens estão errados, pois todos eles cortam a singularidade!
Resposta
- A parte lateral do cilindro , onde