Calcule, onde e é a curva dada pela intersecção de com o plano , orientada de modo que sua projeção no plano seja percorrida no sentido anti-horário.
Passo 1
O que temos é isso aqui:
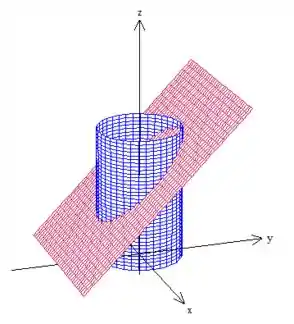
Vamos começar parametrizando essa curva aí, que é dada pela intersecção do cilindro:
Com o plano
No caso, temos uma elipse, não é? Podemos começar parametrizando a projeção no plano em coordenadas polares, já que se trata de uma circunferência de raio :
Agora, nós escrevemos a coordenada usando :
Como gira no sentido anti-horario, .
Passo 2
Agora para pra pensar um pouquinho: imagina quando a gente levar essa parametrização para o campo. Vai ficar um negócio biazarro, né? Vamos ver se dá resolver essa questão por Stokes. Quem sabe...
Olha que lindo essse rotacional zero! Quer dizer que o campo é conservativo! Toma cuidado aqui, ainda temos uma indeterminação em . Vamos com calma então.
Passo 3
O Teorema de Stokes nos diz isso aqui:
Ou seja, podemos substituir essa integral de linha sobre a curva por uma integral do rotacional de sobre uma superfície que tenha a curva como fronteira. Ah, vamos usar o próprio retalho do plano em forma da elipse, né?
Agora vem o momento em que temos que tomar muito cuidado, temos uma intermnação em , ou seja, no eixo .
Então, não podemos usar o plano como superfíce, na verdade, não podemos usar nenhuma superfície que tenha apenas como fronteira por causa disso!
Ferrou, né? Não, vamos usar uma superfície que tenha como uma de suas fronteiras. Em vez de usar o plano, vamos usar esse pedaço do cilindro, que também tem como fronteira.
Então, é o pedaço do cilindro cortado pelo plano e é a própria curva mais a borda debaixo do cilindro (uma circunferência).Temos então:
Como já vimos que o rotacional é nulo:
Agora vamos pensar nas orientações. Se está no sentido anti-horário, pela Regra da Mão direita, deve ter vetor normal apontando para dentro. Consequentemente, gira no sentido horário.
Passo 4
Agora, para terminar a questão, precisamos calcular a integral de linha na outra borda da superfície, .
Como a circunferência está no plano , sua equação é a mesma do cilindro:
Parametrizando isso aí em coordenadas polares com , temos:
Como temos uma volta completa no sentido horário, vai de a .
Essa última componente é porque a curva está no plano .
Certo, agora vamos derivar isso aí:
Agora vamos escrever o campo nas variáveis da parametrização e usar a fórmula:
Levando para a integral, temos:
Lembando que:
Passo 5
Temos então