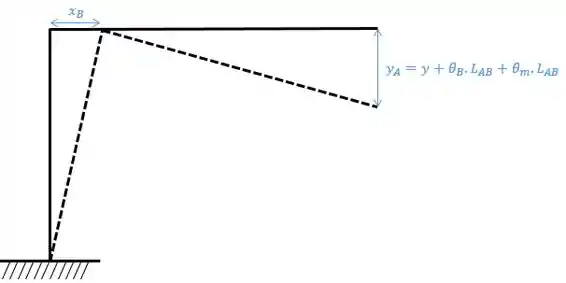
Determine a deflexão vertical e a inclinação na extremidade do suporte. Considere que ele está engastado na base e despreze a deformação axial do segmento . é constante.
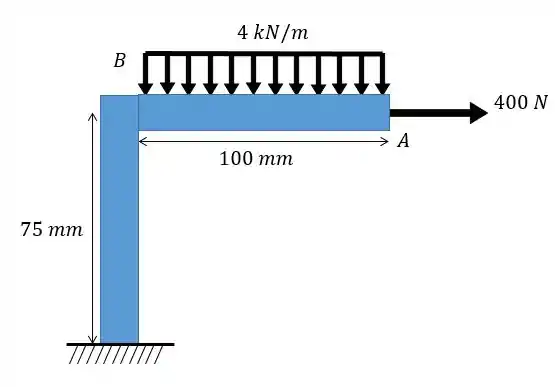
Passo 1
E ai, pessoal!! Essa questão aqui é um pouquinho diferente né? Mas se liga, não é muito mais complicada não porque nós vamos analisar separadamente cada barra. Então vamos ter isso aqui ó:
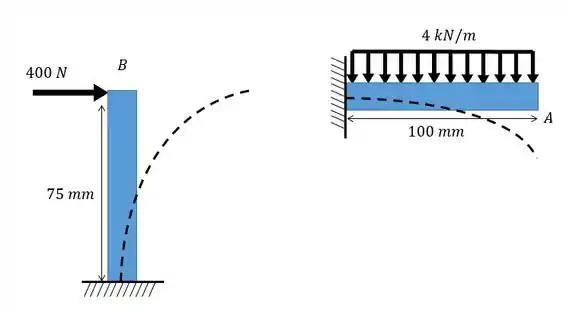
Olha como ficou bem mais simples o problema né? Agora é só fazer cada um separadamente =D
Perceba que quando cortamos a barra a gente tem que introduzir um engaste para que a barra horizontal permanece em equilíbrio! Afinal as duas barras estavam realmente unidas não é mesmo?
Passo 2
Começando pela barra vertical a gente vai ter:
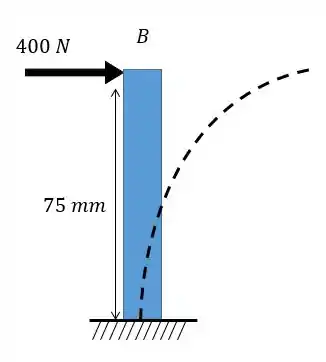
Utilizando a tabelinha:
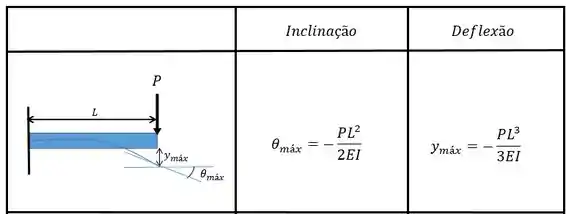
Então podemos substituir os valores para achar a inclinação:
E para a e deflexão:
obs: Reparem que utilizei porque aqui a deflexão é na horizontal!
Passo 3
Agora vamos olhar o trecho horizontal:
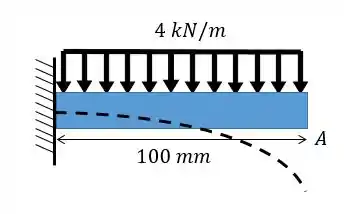
Com a tabela vamos ter:
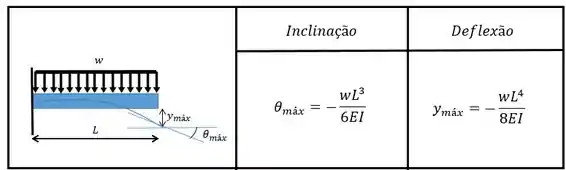
Assim a inclinação será dada por:
E a deflexão:
Passo 4
Agora nós temos de combinar esses valores. Normalmente a gente faria apenas uma soma normal, mas aqui nós temos duas barras diferentes.
Pessoal, a inclinação é mais fácil. É basicamente só somar a inclinação das duas barras. Mas aqui a gente tem que lembrar que o carregamento distribuído vai exercer um momento na barra vertical que não foi contabilizado. Assim devemos incluir uma inclinação , onde:
Logo, somando todos os termos vamos ter:
Para a deflexão: