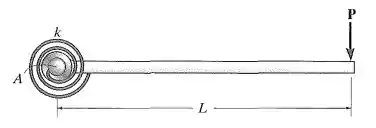
A extremidade da haste está presa por um pino e acoplada a uma mola de torção de rigidez que mede o torque por radiano de rotação da mola. Se uma força for sempre aplicada perpendicularmente à extremidade da haste, determine o deslocamento da força
Passo 1
Galera, essa questão é bem parecida com as que a gente tem feito, a única diferença é que agora tem uma mola de torção. Mas isso não é problema porque podemos utilizar o método da superposição ainda.
Vamos fazer o seguinte, ver o quanto é a deflexão da força , pela tabela. Depois a gente vai somar essa deflexão com a deflexão que ocorreria se existisse apenas a mola!
Partiu resolver!
Passo 2
A primeira coisa é dividir as cargas, vou mostrar isso de forma bem visual para vocês:
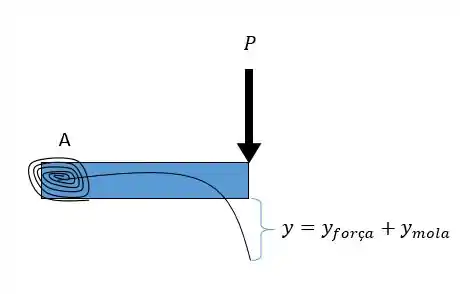
A deflexão causada pela mola pode ser calculada a partir da equação de uma mola de torção onde a torção é igual à constante vezes o ângulo:
Como o torque é igual à força vezes a distância:
Vamos ter que:
Logo a inclinação relativa à mola vai ser de:
Mas não queremos a inclinação, queremos a deflexão, então basta multiplicar pela distância .
Essa deflexão é para baixo!
Passo 3
Agora, com auxilio da tabela, vamos calcular a deflexão por causa da força :
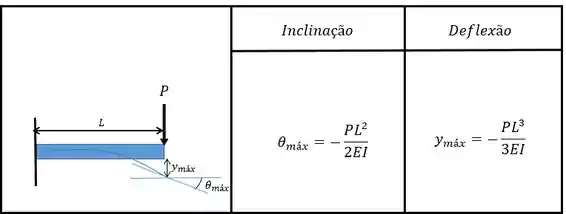
Assim vamos ter
Podemos escrever como um deslocamento positivo mas para baixo:
Passo 4
Agora é só somar essas deflexões:
para baixo.
Resposta
para baixo.