Determine o momento em termos da carga e a dimensão de modo que a deflexão no centro da viga seja nula. constante.
Passo 1
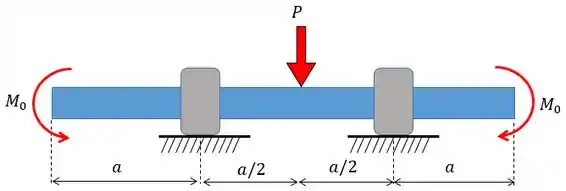
Faaala, galerinha!! Esse problema nos fornece um eixo com dois apoios e com uma força e dois momentos atuantes. Para resolver isso e achar o valor de e de forma que a deflexão no centro seja nula a gente vai fazer separadamente:
- A deflexão causada pela força .
- A deflexão causada pelos momentos .
A soma dessas deflexões deve ser zero. Importante lembrar que vamos fazer isso utilizando as tabelas.
Passo 2
A primeira coisa é dividir as cargas, vou mostrar isso de forma bem visual para vocês:
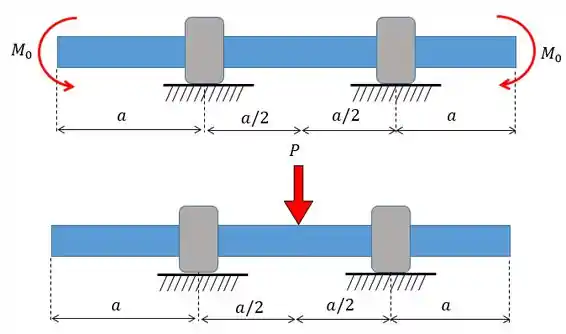
Bem tranquilo né? Só separar cada carga em um desenho.
Passo 3
Agora, com auxilio da tabela, vamos calcular a deflexão por causa da força :
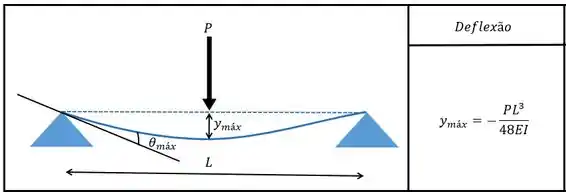
Perceba que as partes externas do nosso eixo não influenciam agora então vamos olhar apenas a parte interna e a nossa equação é:
Substituindo os valores vamos ter:
Show! Essa é a deflexão causada pela força .
Passo 4
Agora vamos olhar a deflexão causada pelos momentos, mas não existe nenhuma tabela com a mesma configuração do nosso problema. O que temos é essa aqui:
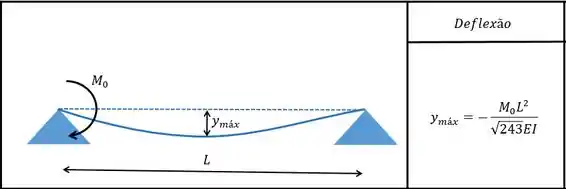
Aí agora a gente tem que fazer uma sacação bolada para sair do que temos e chegar em algo parecido com isso aí! O que a gente tinha era o seguinte:
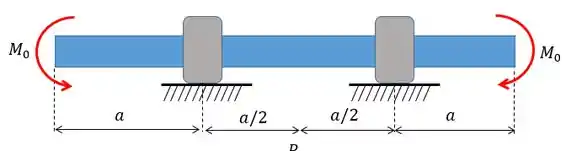
Nesse caso o momento fletor acaba sendo constante por todo o eixo e vale exatamente , logo podemos transformar o carregamento a cima em:
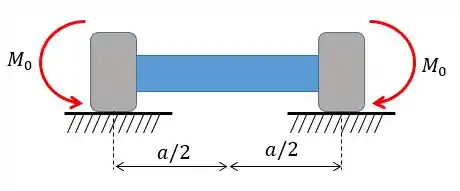
E pronto! Chegamos num desenho igual ao da tabela (lembre que os apoios aqui são de segundo gênero também). Temos que ver também que temos dois momentos ao invés de apenas um e que eles têm sentido oposto ao da tabela então deveremos mudar o sinal. Assim, vamos obter:
Como
Passo 5
Agora é só somar ambos os valores:
Referente à força:
Referente aos momentos:
Esse valor é aproximadamente
Resposta
Que é aproximadamente: