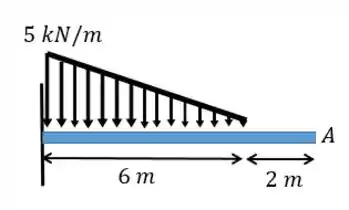
Determine o deslocamento e a inclinação em . Considere constante.
Passo 1
Fala aí, pessoal!! Para resolver essa questão a gente só precisa ir na nossa tabela de inclinações e deflexões de vigas em balanço e achar o respectivo carregamento!
Dessa vez a gente vai ver que esse carregamento triangular que é finalizado no meio da viga não existe na tabela. Então vamos utilizar ainda a tabela mas para saber o valor exato vamos aplicar também alguns conceitos de geometria, vem comigo!
Passo 2
A nossa tabela nos fornece:
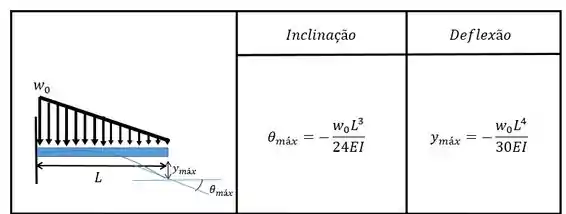
Como dito anteriormente esse não é o carregamento exatamente igual ao do problema. Mas aí que vai entrar a geometria. Vamos olhar o nosso carregamento original:
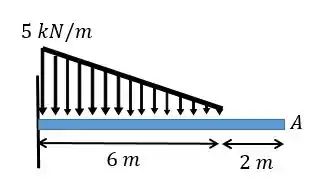
Perceba que quando o carregamento cessa não há mais forças atuando na viga. Por esse motivo a inclinação da viga permanecerá constante. Assim se acharmos a inclinação da viga ao final do carregamento essa inclinação será a mesma em também!
Passo 3
Como a gente tem que a inclinação é constante, para achar a deflexão basta multiplicar a inclinação pela distância até a ponto . E temos de considerar também a deflexão máxima, que é somada a isso tudo.
Resposta
Podemos expressar em módulo indicando o sentido:
para baixo.