Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Superposição de efeitos

Ver Teoria
Exercício 31245678

Enunciado

A viga simplesmente apoiada com perfil W 360 × 64 feita de aço A - 36 é submetida à carga mostrada na figura. Determine a deflexão em seu centro C .

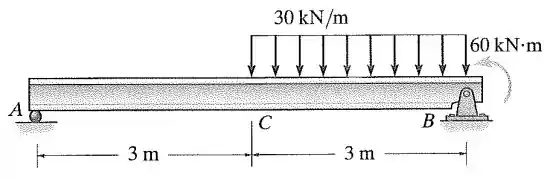
Passo 1

Fala aí, pessoal!! Para resolver essa questão utilizando o método da superposição dos efeitos a gente precisa fazer duas coisas basicamente.

  1. Dividir as duas cargas aplicadas na viga. Essas cargas são: a carga distribuída de 30   k N / m e o momento puro de 60   k N . m .
  2. Calcular, por meio da tabelinha, a deflexão de cada carga e realizar a soma algébrica dessas deflexões.

Beleza? Vamos fazer isso aí então.

Passo 2

A primeira coisa é dividir as cargas, vou mostrar isso de forma bem visual para vocês:

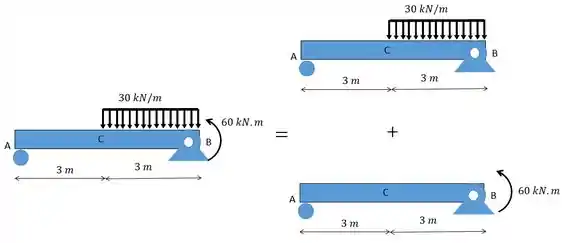
Pronto! Esse passo é bem simples não é mesmo? Só dividir cada carregamento em desenhos separados.

Passo 3

Agora, com auxilio da tabela, vamos calcular a deflexão no ponto A :

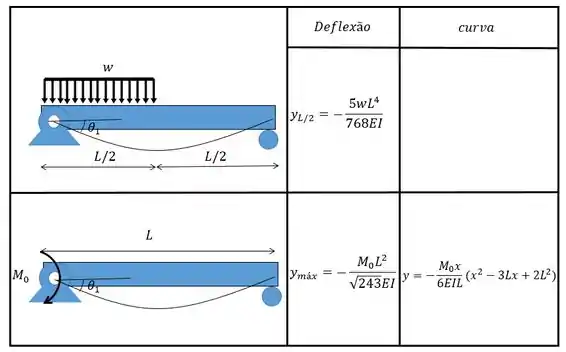
Como queremos no ponto C que é o centro vamos ter que a deflexão causada pela carga distribuída vale:

y d i s t r i b u i d a = - 5 30000 6 4 768 E I

y d i s t r i b u i d a = - 253125 E I

Perceba que a tabela já nos fornece a deflexão no ponto médio. Desta forma não precisamos substituir na equação da curva, diferentemente do momento.

E para o momento puro:

y m o m e n t o = - M 0 x 6 E I L ( x 2 - 3 L x + 2 L 2 )

y m o m e n t o = - M 0 L 2 6 E I L L 2 2 - 3 L L 2 + 2 L 2

y m o m e n t o = - M 0 12 E I L 2 4 - 3 L 2 2 + 2 L 2

y m o m e n t o = - M 0 12 E I L 2 4 - 6 L 2 4 + 8 L 2 4

y m o m e n t o = - M 0 12 E I 3 L 2 4

Agora podemos substituir:

y m o m e n t o = - ( 60000 ) 12 E I 3 ( 6 ) 2 4

y m o m e n t o = - 135000 E I

obs: Aqui é válido notar que tanto o momento do nosso problema quanto o momento da tabela geram deflexões negativas ok? Ambos estão no mesmo sentido.

Outra coisa legal de ver é que apesar de na tabela parecer que as cargas estão na outra extremidade da viga é só a gente olhar a viga pelo outro lado e verificar que as cargas na verdade são idênticas.

Passo 4

Agora é só somar essas deflexões:

y C = y d i s t r i b u i d a + y m o m e n t o

y C = - 253125 E I - 135000 E I

y C = - 388125 E I

Agora só falta substituir E e I . Mas isso é tranquilo..

Como o aço é o A - 36 então:

E = 200   G P a

E como é um perfil W   360 × 64 então:

I = 179 × 10 6   m m 4

I = 179 × 10 - 6   m 4

Substituindo na nossa equação:

y C = - 266981 E I

y C = - 388125 ( 200 × 10 9 ) ( 179 × 10 - 6 )

y C = - 10,84   m m

Ou

y C = 10,84   m m

Para baixo

Resposta

y C = - 10,84   m m

Ou

y C = 10,84   m m

Para baixo

Exercícios de Livros Relacionados

Para a viga uniforme em balanço e o carregamento mostrados nas figuras, determine a inclinação e a deflexão no (a) ponto B e no (b) ponto C.
Uma barra de 16 mm de diâmetro foi moldada assumindo a forma mostrada. Determine a deflexão da extremidade C após lhe ser aplicada uma carga de 200 N. Use E = 200 GPa e G = 80 GPa.
Para a viga prismática e o carregamento mostrados nas figuras, determine (a) a inclinação na extremidade A e (b) a deflexão no centro C da viga.
Para a viga e o carregamento indicado, determinar a intensidade e a localização da maior deflexão dirigida para baixo.A intensidade do máximo para a Viga e carregamento do P r o b . 9 . 57 .
Para a viga com o carregamento mostrado, determinar a reação de apoio móvel.Obs: determinação dos valores da viga no estado isostático para o caso 1