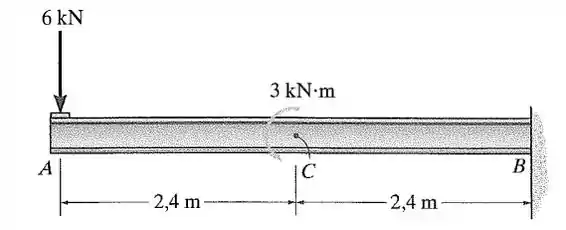
A viga em balanço com perfil feita de aço é submetida à carga mostrada na figura. Determine o deslocamento em sua extremidade .
Passo 1
Fala aí, pessoal!! Para resolver essa questão utilizando o método da superposição dos efeitos a gente precisa fazer duas coisas basicamente.
- Dividir as duas cargas aplicadas na viga. Essas cargas são: a força de e o momento puro de .
- Calcular, por meio da tabelinha, a deflexão de cada carga e realizar a soma algébrica dessas deflexões.
Beleza? Vamos fazer isso aí então.
Passo 2
A primeira coisa é dividir as cargas, vou mostrar isso de forma bem visual para vocês:
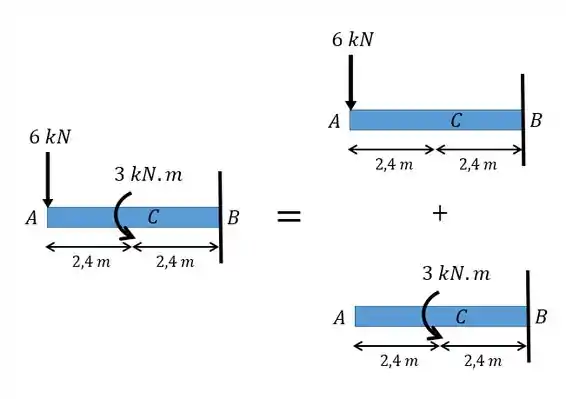
Pronto! Esse passo é bem simples não é mesmo? Só dividir cada carregamento em desenhos separados.
Passo 3
Agora, com auxilio da tabela, vamos calcular a deflexão no ponto :
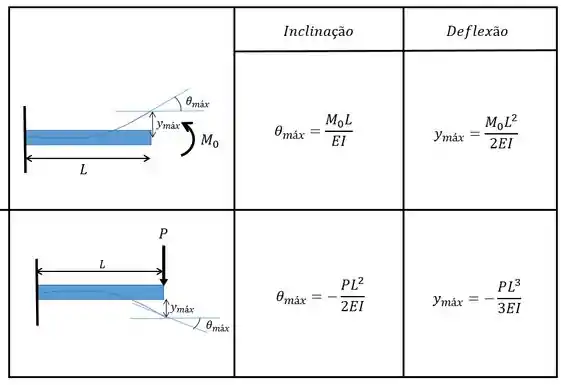
Pela tabela vamos ter que a deflexão causada pela força de será de:
Como e , vamos ter:
Agora para o momento puro:
Como e vamos ter:
obs: Reparem que utilizamos o comprimento de onde efetivamente o momento é aplicado, que é o ponto , mas não queremos no ponto queremos no ponto .
Logo, para resolver essa questão a gente tem que fazer o seguinte: Perceber que depois da carga a inclinação continua constante. Se a inclinação continua constante a deflexão varia linearmente. Assim a deflexão em , causada pelo momento, vai ser:
Faz sentido, não faz? Se a inclinação é constante, então a deflexão terá de ser o dobro quando também é dobrado!
Passo 4
Agora é só somar essas deflexões:
Agora só falta substituir e . Mas isso é tranquilo..
Como o aço é o então:
E como é um perfil então:
Substituindo na nossa equação:
Resposta
Ou
Para baixo