Considere definida por . Na figura abaixo, representa a área da região indicada e é a área do triângulo com vértices em , e indicado.
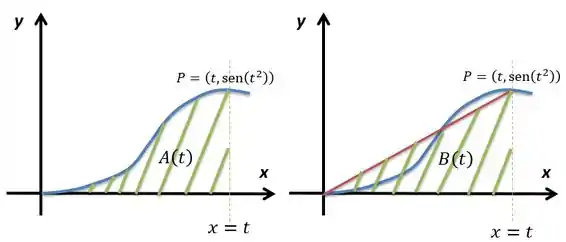
Determine .
Passo 1
Aeee. Finalmente uma questão diferentona!!
Vamos resolver essa questão com calma, começando primeiro definindo quem seriam esses e , porque só assim poderemos definir nossa estratégia de resolução, não é mesmo?
Segundo a primeira imagem, é a área de de até um ponto qualquer. Seria isso daqui:
Já o é simplesmente a área do triângulo com um vértice na origem, um em e outro em . Sua base é e sua altura é , então a área do triângulo será:
Assim, o limite que nos interessa é:
Passo 2
Bem, em tããão diferentona assim, né não?
Temos de novo aquela velha história de um limite misturado com uma integral. Como sempre, vamos substituir e ver o que acontece:
Já sabemos que integral com limites de integração iguais é nula. Então, adivinha? Caímos numa indeterminação do tipo:
Passo 3
Assim, como caímos numa indeterminação, podemos usar L’Hospital:
Bem, para o numerador, vamos usar o Teorema Fundamental do Cálculo; para o denominador usamos a Regra do Produto:
Passo 4
Vou calcular o inverso desse limite (deixando o de lado por enquanto) e depois eu desinverto o resultado e jogo nessa última expressão que achamos.
Vamos concentrar só nesse limite que sobrou:
Podemos usar L’Hospital nele, já que caímos em outra indeterminação:
Passo 5
Muita calma nessa hora pra não se confundir. Lembrando, vimos que a resposta da questão é:
Deixamos o 2 de lado, e focamos no limite
E a gente viu que o inverso desse limite é:
Ou seja, desinvertendo:
Agora é só multiplicar por 2 pra chegar na resposta final:
E essa é, finalmente, a nossa resposta! :)