O discriminante é zero na origem pra cada uma das funções a seguir, de modo que o teste da derivada segunda falha. Determine se a função tem um máximo, um mínimo ou nenhum dos dois na origem, imaginando como é a superfície . Descreva seu raciocínio em cada caso.

a)

b)

b)

Agora complicou um pouco! Dessa vez temos

Não podemos afirmar nada do sinal da função tão facilmente quanto fizemos pra função anterior.

Agora vamos ter que dividir nosso estudo da função em vários casos.

A ideia vai ser tentar mostrar que num deles a origem seria um ponto de máximo, e em outro ela seria um ponto de mínimo. Se isso acontecer, poderemos concluir que ela não é nem um nem outro.

Comecemos pelo caso mais simples, em que consideramos e . Pense que a gente está se aproximando da origem pelo 1º quadrante.

Assim temos e . Agora ficou bem parecido com a letra (a) né?

Então nesse caso a origem seria um ponto de mínimo.

Agora vamos tentar achar uma abordagem da função pra qual a origem seria um ponto de máximo, beleza? O macete é a gente pensar ao contrário! Queremos:

Portanto, e devem ter sinais opostos, por exemplo e . Assim, e . Então agora estamos nos aproximando da origem pelo 2º quadrante. E verificamos que nesse caso temos .

Então nesse caso a origem seria um ponto de máximo. Sendo que vimos um outro caso em que ela seria um ponto de mínimo.

Portanto, podemos concluir que ela não é nem máximo e nem mínimo!

Um passinho bônus só pra mostrar o mapa de contorno da função:

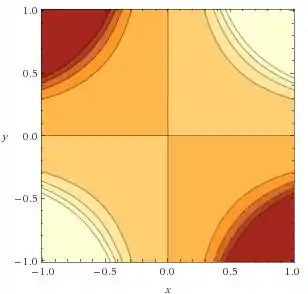
Repare como o 1º e o 3º quadrantes têm uma cor mais clara do que o 2º e o 4º, perto da origem, e como a mudança de cor é brusca.