Seja . Então :
(a) nenhuma das outras alternativas
(b) é ponto crítico e ponto de sela.
(c) é ponto crítico e ponto de mínimo local.
(d) é ponto crítico e ponto de máximo local.
(e) não é ponto crítico.
Passo 1
Vamos começar testando se é um ponto crítico, que tal?
As derivadas parciais em dão zero, então é um ponto crítico! Já dá até pra eliminar a alternativa (e).
Passo 2
Vamos tentar classificar o ponto com o teste da derivada segunda. Então vamos calcular as derivadas de segunda ordem!
Passo 3
Vamos ao teste da derivada segunda: no ponto temos
Vish, já dá pra ver que tem algo estranho. O determinante vai ser
Pois é, o determinante deu , que é justamente o caso que a gente não sabe classificar o ponto crítico!
Passo 4
Essa é hora que você tem que parar pra analisar a função friamente:
Vamos tentar visualizar a superfície que é o gráfico dessa função.
Estamos interessados no ponto , e esse ponto faz parte do plano , certo? No plano temos
e isso a gente sabe que é uma parábola voltada pra cima. Então nesse plano o ponto é um ponto de mínimo:
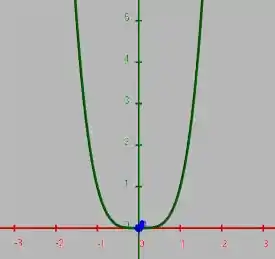
E se olharmos no plano temos
que é uma parábola voltada pra baixo, então esse plano o ponto é um ponto de máximo!
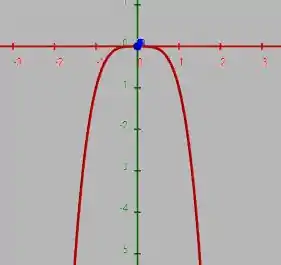
Então não tem como o ponto ser um ponto de máximo ou mínimo da função, ele é um ponto de sela!
Observação: Essa função parece muito com a equação do paraboloide hiperbólico, vulga “sela”:
Olha como é que é o gráfico da função: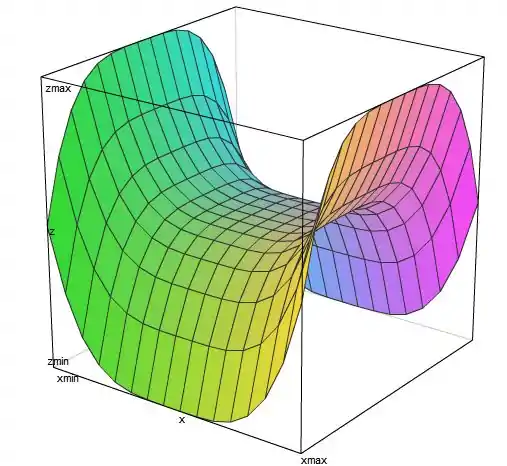
Resposta
Alternativa (b)