Seja . Então :
(a) é ponto crítico e ponto de sela;
(b) é ponto crítico e ponto de mínimo local;
(c) não é ponto crítico
(d) é ponto crítico e ponto de máximo local;
(e) nenhuma das anteriores;
Passo 1
Vamos começar determinando se o ponto é um ponto crítico:
Então o ponto é um ponto crítico, já podemos eliminar a alternativa (c).
Passo 2
Agora vamos calcular as derivadas segundas:
Pronto! Agora podemos aplicar o teste da derivada segunda:
Vish! Deu ruim! A gente sabe como classificar o ponto se o determinante for maior ou menor que zero, mas e quando dá zero? Senta e chora? Nada disso! Vamos simplesmente parar pra olhar a função com calma.
Temos a soma de e , ambos elevados a potências pares. E a gente sabe que
Também podemos dizer , logo e .
De qualquer forma, chegamos à conclusão que o ponto é ponto de mínimo global de . Mas como todo ponto de mínimo global é também ponto de mínimo local (o contrário é falso), a alternativa (b) é a certa.
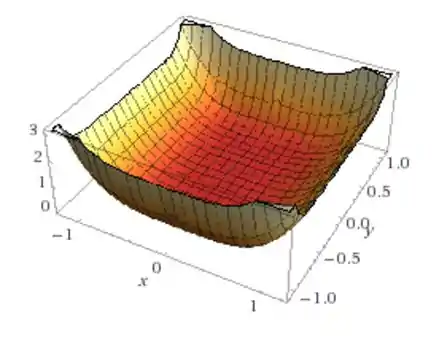
A gente pode até dar uma olhada no gráfico da função:
Resposta
Alternativa (b)