Defina uma regra de decisão para decidir entre as seguintes hipóteses sobre a origem das peças de uma amostra que vão ser usadas numa fábrica:
Defina também a região crítica do seu teste de hipóteses.
Passo 1
A regra de decisão é sempre tomada a partir da nossa amostra. Se nossos testes envolvem o desvio padrão populacional , o parâmetro amostral que vamos usar na regra de decisão é o , que é o desvio padrão amostral.
Podemos tomar qualquer regra de decisão que seja minimamente conveniente. Por exemplo, nós sabemos que o desvio padrão populacional ser , significa que as peças tem origem A. Mas pode acontecer das peças da nossa terem origem A mas fugirem um pouquinho de , certo? Tipo, serem . Por que podem fugir? Porque é uma amostra, e erros sempre acontecem!
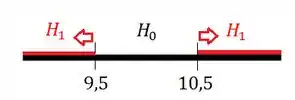
Então vamos estipular uma margem de erro qualquer para englobar possíveis erros do tipo. Vamos dizer que se o desvio padrão amostral estiver entre e , vamos tomar a decisão de que as peças da amostra tem origem A, estamos considerando então uma margem de erro de :
E para o contrário, vamos aceitar a hipótese alternativa:
Essas aí são possíveis regras de decisão que poderíamos tomar.
Passo 2
A região crítica é onde rejeitamos a hipótese nula, ou seja, é a região da regra de decisão que acabamos de descrever para quando aceitamos a hipótese alternativa:
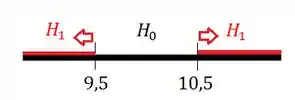
Essa área vermelha aí então é nossa
Resposta