Para o teste de hipótese de média para grandes amostras, especifique os testes para os 3 casos discutidos nas transparências ao nível de confiança de , hipótese nula e a hipótese alternativa, e mostre através de gráficos as regiões de aceitação e de rejeição dos testes.
Passo 1
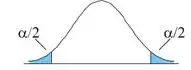
No teste bilateral, queremos verificar se a média populacional é igual ou não a um certo valor. As hipóteses são:
No gráfico, temos em azul as regiões de rejeição, e em branco a região de aceitação:
Passo 2
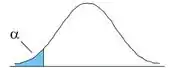
No teste unilateral inferior, queremos verificar se a média populacional é menor que um certo valor. As hipóteses são:
No gráfico, temos em azul a região de rejeição, e em branco a região de aceitação:
Passo 3
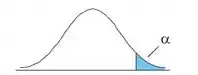
No teste unilateral superior, queremos verificar se a média populacional é maior que um certo valor. As hipóteses são:
No gráfico, temos em azul a região de rejeição, e em branco a região de aceitação:
Resposta
Ei, a resposta está no passo a passo :)