A variável X, custo de manutenção de um tear, pode ser considerada como tendo distribuição normal de média e desvio padrão 20 unidades. Os valores possíveis de podem ser 200 ou 210. Para verificar qual dos dois é o mais provável, utiliza-se uma amostra de 25 teares. Defina:
a) Uma hipótese a ser estudada
b) Uma regra de decisão.
Passo 1
Vamos analisar a letra a)
Bom, nós temos 3 tipos diferentes de hipóteses: BILATERAL,UNILATERAL INFERIOR e UNILATERAL SUPERIOR.
Quem decide o tipo de teste é o sinal usado na construção da hipótese alternativa!
Se for é bilateral, se for é unilateral inferior e se for é unilateral superior!
Como o enunciado não diz nada diferente, podemos escolher de forma aleatória, concorda?! Então:
Beleza?!
Passo 2
b) Uma regra de decisão.
Vamos lá!! Como definir a regra de decisão?
Cara, a regra de decisão nada mais é do que definir, com base em nossa amostra, qual hipótese estava correta.
Uma possibilidade: Como estamos trabalhando com os valores 210 e 210, vamos escolher o ponto médio 205 como ponto crítico. Assim,
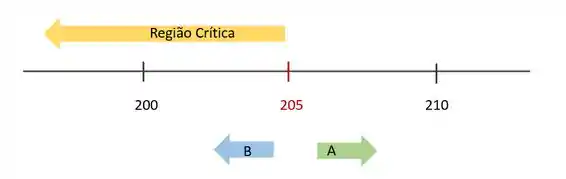
Ou seja, se a minha média amostral cair pra cima de 205 eu tenho que o produtor será , da mesma forma, se ele cair pra baixo ele vai ser do produtor
Lembrando que a região crítica é aquela que nos leva a rejeitar e aceitar . Vai ser sempre assim, não esquece isso!
Resposta
Ei, a resposta está no passo a passo :)