a) Em um teste de hipótese, como se definem os parâmetros: alfa (probabilidade do erro tipo I) e beta (probabilidade do erro tipo II)?
b) Seja uma variável aleatória normal com média e variância , e uma variável aleatória qui-quadrado (). Se compararmos as curvas das funções densidade de probabilidade desta normal e da distribuição qui-quadrado com e graus de liberdade, qual destas duas últimas curvas está mais próxima de ter um coeficiente de simetria igual a zero? Esboce em um mesmo gráfico as três curvas.
Passo 1
Eai galerinha, beleza? Bora para mais uma questão de PROBEST!
O item (a) é totalmente teórico, não vamos fazer nenhuma conta! Ele pede simplesmente para conceituarmos os parâmetros alfa e beta nos testes de hipótese. Para isso, vou fazer uma pequena digressão...
Quando fazemos um teste de hipótese, queremos verificar se ela é verdadeira ou falsa. Se a hipótese for válida e nosso teste verificar isso, o teste deu bom. Se a hipótese for furada e o teste prever isso, também deu bom. Mas e se a hipótese for válida, porém o teste dizer que ela não é? Aí deu ruim...
Os dois erros que podemos cometer em um teste de hipótese são:
(i) rejeitar uma hipótese quando ela é verdadeira.
(ii) não rejeitar a hipótese quando ela deve ser rejeitada.
O primeiro erro é chamado erro do tipo I e o segundo é chamado de erro do tipo II. Os parâmetros alfa e beta são as probabilidades desses erros acontecerem.
Portanto, alfa é a probabilidade de o teste concluir que uma hipótese não é válida quando na verdade ela é, enquanto beta é a probabilidade de o teste não rejeitar uma hipótese quando ela deveria ser rejeitada.
A situação ideal para um teste de hipótese é aquela em que alfa e beta são o mais próximo de zero possível, o que significa que as chances de erro (de qualquer tipo) do teste são baixas.
Passo 2
O item (a) foi bem simples, era só saber bem a teoria por trás dos testes de hipótese. Agora vamos para o item (b), que também é bem teórico, só que dessa vez sobre a distribuição de qui-quadrado.
A seguir faço o plot da distribuição de qui-quadrado para alguns graus de liberdade:
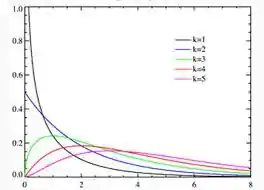
Conforme o número de graus de liberdade aumenta, as curvas vão ficando cada vez mais simétricas e se aproximam de uma gaussiana. Para graus de liberdade:

Relaxa que você não precisava saber fazer o plot dessas curvas, eu fiz só por ilustração: o que você precisa saber é a tendência delas conforme o número de graus de liberdade aumenta!
Entre as curvas com e graus de liberdade, a distribuição com dois graus de liberdade será mais simétrica. A seguir faço o esboço das três curvas:
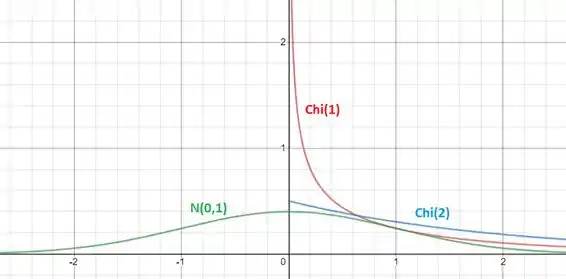
A curva de qui-quadrado com tem coeficiente de simetria mais próximo de zero, já que ela é mais simétrica e se aproxima mais da curva gaussiana.
Com isso terminamos o problema 😊
Resposta
a) Alfa é a probabilidade de o teste concluir que uma hipótese não é válida quando na verdade ela é, enquanto beta é a probabilidade de o teste não rejeitar uma hipótese quando ela deveria ser rejeitada.
b) .