Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Tipos de Funções de Várias Variáveis

Ver Teoria
Exercício 213456789101112131415161718

Enunciado

UFABC. Cálculo. Funções de Várias Variáveis. Lista 7 – Integrais Triplas. Questão 2d.

2 - A área de uma superfície determinada pelo gráfico de uma função de duas variáveis z = f x , y definida numa região R ⊂ R 2 é dada pela fórmula

A = ∫ ∫ R 1 + ∇ f x , y 2 d A

Se f é dada implicitamente pela equação F x , y , z = 0 , então

A = ∫ ∫ R ∇ F x , y , z ∂ F x , y , z ∂ z d A

onde z = f x , y e supondo que nesse caso ∂ F x , y , z ∂ z ≠ 0 no interior de R . Determine a área das seguintes superfícies:

d) A parte da esfera x 2 + y 2 + z 2 = a 2 que está dentro do cilindro x 2 + y 2 = a x e acima do plano x y .

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão temos uma forma diferente de calcular a área de uma superfície limitada por uma região R .

A ideia é calcular a área da esfera x 2 + y 2 + z 2 = a 2 que está dentro do cilindro x 2 + y 2 = a x e acima do plano x y , ou seja, a parte positiva de z .

Mas como fazemos isso? 🤔

Pra isso, o enunciado nos deu uma equação que justamente nos descreve a área que queremos

A = ∫ ∫ R 1 + ∇ f x , y 2 d A

O que temos que fazer é calcular o gradiente de f e obter seu módulo.

Lembrando que z = f x , y , então

z = a 2 - x 2 - y 2

Assim substituímos na integral!

Quer ver? Bora começar! 😎

Passo 2

Primeiro vamos calcular o gradiente de f .

∇ F x , y = ∂ f ∂ x , ∂ f ∂ y

Derivando f em função de x , pela regra da cadeia.

∂ f ∂ x = ∂ a 2 - x 2 - y 2 ∂ x

∂ f ∂ x = - x a 2 - x 2 - y 2

Derivando f em função de y , pela mesma regra.

∂ f ∂ y = ∂ a 2 - x 2 - y 2 ∂ y

∂ f ∂ y = - y a 2 - x 2 - y 2

Com isso, o gradiente de f é

∇ F x , y = - x a 2 - x 2 - y 2 , - y a 2 - x 2 - y 2

Obtendo o modulo desse vetor, temos

∇ F x , y = - x a 2 - x 2 - y 2 2 + - y a 2 - x 2 - y 2 2

Se elevarmos este modulo ao quadrado, temos

∇ F x , y 2 = - x a 2 - x 2 - y 2 2 + - y a 2 - x 2 - y 2 2 2

∇ F x , y 2 = x 2 a 2 - x 2 - y 2 + y ² a 2 - x 2 - y 2

∇ F x , y 2 = x 2 + y 2 a 2 - x 2 - y 2

Tranquilo até aqui? 👀

Passo 3

Com isso, nossa função de integração vai ser

1 + ∇ f x , y 2 = 1 + x 2 + y 2 a 2 - x 2 - y 2

Simplificando esse resultado, temos

1 + ∇ f x , y 2 = a 2 - x 2 - y 2 a 2 - x 2 - y 2 + x 2 + y 2 a 2 - x 2 - y 2

1 + ∇ f x , y 2 = a 2 - x 2 - y 2 + x 2 + y 2 a 2 - x 2 - y 2

1 + ∇ f x , y 2 = a 2 a 2 - x 2 - y 2

Logo, temos

1 + ∇ f x , y 2 = a a 2 - x 2 + y 2

Agora vamos olhar para o limite de integração.

Queremos apenas a parte da espera que está dentro do cilindro x 2 + y 2 = a x .

Qual é a projeção de um cilindro visto de cima?

Um círculo, não é?

Com isso, vamos trabalhar com coordenadas polares.

Lembrando que x vira r c o s θ , y vira r s e n θ e x 2 + y 2 vira r 2 .

Escrevendo x 2 + y 2 = a x no plano, vamos ter

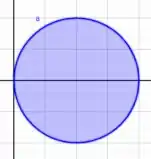
Temos uma circunferência de raio a centrada em x = a e y = 0 .

Ou seja, nosso raio varia de 0 até

r 2 = a r c o s θ

r = a c o s θ

Já nosso θ de π / 2 a - π / 2 , concorda? Já que esse é a variação angular que nossa região R faz com a origem.

Interessante, não é? 😁

Passo 4

Com isso, vemos que os limites de integração de d r é de 0 a a c o s θ e os limites de integração em d θ é de π / 2 a - π / 2 .

Portanto, como o jacobiano para integrais polares é r , nossa integral será

∫ - π 2 π 2 ∫ 0 acos ⁡ θ a r a 2 - r 2 d r d θ

Primeiro vamos integrar com relação a r

∫ a r a 2 - r 2 d r → a ∫ r a 2 - r 2 d r

Pelo método de substituição u d u onde u = a 2 - r 2 , d u d x = - 2 r e d x = - 1 2 r d u

a ∫ - 1 2 1 u d r → - a 2 ∫ 1 u d r = - a 2 2 u 1 2

Substituindo u de volta

∫ a r a 2 - r 2 d r = - a a 2 - r 2

Aplicando os limites de integração, temos

∫ 0 acos ⁡ θ a r a 2 - r 2 d r = - a a 2 - acos ⁡ θ 2 - - a a 2 - 0 2

∫ 0 acos ⁡ θ a r a 2 - r 2 d r = a 2 - a a 2 1 - cos 2 ⁡ θ

Simplificando um pouco mais, temos

∫ 0 acos ⁡ θ a r a 2 - r 2 d r = a 2 - a 2 1 - cos 2 ⁡ θ

∫ 0 acos ⁡ θ a r a 2 - r 2 d r = a 2 - a 2 s e n 2 θ

∫ 0 acos ⁡ θ a r a 2 - r 2 d r = a 2 - a 2 s e n θ

Bacana, não é?

Passo 5

Com base no resultado anterior, integramos com relação a θ

∫ a 2 - a 2 s e n θ d θ

Como a é uma constante e a integral de uma constante é igual a constante multiplicada pela variável de integração.

Já a integral do s e n é igual a - c o s pelo teorema fundamental do cálculo.

∫ a 2 - a 2 s e n θ d θ = a 2 θ + a 2 cos ⁡ θ

Aplicando os limites de integração, temos

∫ - π 2 π 2 a 2 - a 2 s e n θ d θ = a 2 π 2 + a 2 cos ⁡ π 2 - a 2 - π 2 + a 2 cos ⁡ - π 2

∫ - π 2 π 2 a 2 - a 2 s e n θ d θ = π a 2 2 + π a 2 2

∫ 0 2 π a 2 - a 2 s e n θ d θ = π a 2

Com isso, descobrimos que a superfície da esfera que está contida acima do plano x y e dentro do cilindro x 2 + y 2 = a x possui área de π a 2

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

π a 2

Exercícios de Livros Relacionados

37. Para as funções de uma variável, é impossível uma função continua ter dois pontos de máximo local e nenhum ponto de mínimo local. Para funções de duas variáveis, esse caso existe. Mostre que a fun