UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cálculo 2 - Profº Ronie Peterson - Lista de Exercícios 1, Questão 2d
O índice de sensação térmica, denotado por , mede a temperatura subjetiva que depende da temperatura real e da velocidade do vento, , ou seja, é uma função . A tabela abaixo apresenta valores de compilados pelo Serviço Nacional de Meteorologia dos Estados Unidos e pelo Serviço Meteorológico do Canadá.
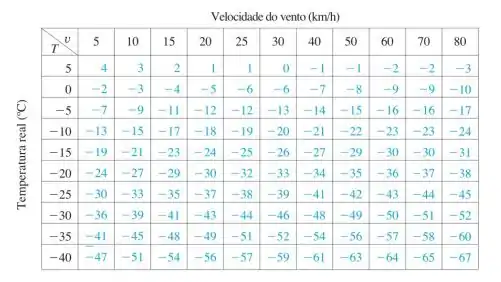
- O índice foi modelado pela função . Verifique quão próximo este modelo está dos valores da tabela para alguns valores de e . PS: Utilize calculadora ou recurso computacional.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma tabela que determina o índice de sensação térmica em função da temperatura e da velocidade do vento .
A questão nos dá a fórmula do índice dada por:
E pede para compararmos com os valores da tabela.
Uma forma de proceder é pegar alguns valores de e , substituir na fórmula e comparar com os valores da tabela.
Não entendeu? Então bora junto aqui!!
Passo 2
Dessa forma, vamos pegar alguns valores e aplicar na fórmula:
- Para :
- Para :
- Para :
Comparando com o valor da tabela, temos .
Comparando com o valor da tabela, temos .
Comparando com o valor da tabela, temos .
Assim, podemos perceber que os valores se diferenciam apenas por algumas casas decimais.
Entendeu direitinho? Responde aee ;)
Resposta
No texto