Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Tipos de Funções de Várias Variáveis

Ver Teoria
Exercício 312456789101112131415161718

Enunciado

Livro James Stewart, Volume 2, 7ª Edição, Capítulo 14, Seção 1, Exercício 10

(Cap. 14.1 - Ex. 10) Seja F x , y = 1 + 4 - y 2 .

(a) Calcule F ( 3,1 ) .

(b) Determine e esboce o domínio de F .

(c) Determine a imagem de F .

Passo 1

Falaaa aí! Tudo joinha? Bora lá resolver mais uma questão?

Esse exercício aqui, é dividido em 3 itens (a), (b) e (c), então nós vamos fazer um de cada vez, combinado?

O item (a), pede pra gente quer calcular F ( 3,1 ) . Isso significa que a gente vai substituir x = 3 e y = 1 na nossa função F ( x , y ) , beleza? Vamos lá então!

Nossa função é: F x , y = 1 + 4 - y 2 . Maaaas... não tem x nela!! Onde que a gente vai substituir x = 3 ?

Bom, a gente não vai! Se não tem o x ali, não se preocupe com ele. Vamos substituir só o y ...

F 3,1 = 1 + 4 - 1 2

F ( 3,1 ) = 1 + 3

Prontinho! Item (a) resolvido! Bem simples, né?

Passo 2

Agora vamos pro item (b).

Esse item pede pra gente encontrar o domínio da função F . E o que isso significa? O domínio de uma função, nada mais é do que o conjunto de todas as entradas possíveis da função. Por exemplo, o domínio de uma função do tipo f x = x 2 são todos os números reais. Já o domínio de uma função do tipo f x = 1 / x , são todos os reais, com exceção de 0 . E assim por diante...

Bora lá encontrar o domínio então? Antes de começarmos, vamos reescrever nossa função para ficar mais organizada:

z = 1 + 4 - y 2

Agora vamos notar uma coisa. Qual restrição a gente tem aqui? A raiz quadrada não pode ser negativa, não é?

Ou seja, a gente precisa que:

4 - y 2 ≥ 0

- y 2 ≥ - 4

y 2 ≤ 4

y ≥ - 2     e   y ≤ 2

Como o x   não tá na função, ele pode assumir qualquer valor.

Então essa relaçãozinha que fizemos pra y será nosso domínio!! Então:

D = { x , y | 4 - y 2 ≥ 0 } → { ( x , y ) | x ∈ R ,   y ∈ - 2,2 }

Mais simples do que você imaginou, não é mesmo?

O esboço dele ficará da seguinte maneira:

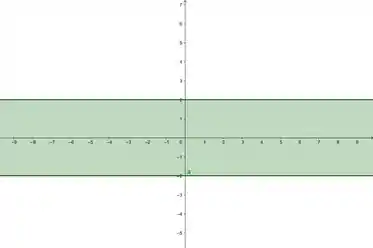
Ou, em 3 D :

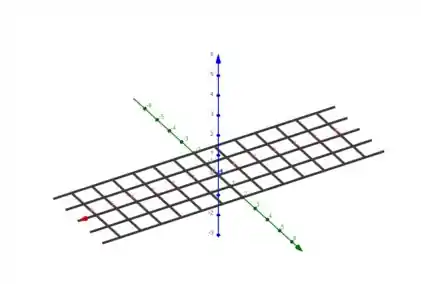
Passo 3

Por fim, vamos fazer o item (c) agora. Esse item nos pede pra encontrar a imagem. Mas o que é a imagem de uma função? O conjunto imagem de uma função, é um subconjunto do contradomínio, formado por todos os elementos correspondentes de algum elemento do domínio. Vamos encontrar a imagem da nossa função que essa ideia vai ficar mais clara!

Bom, vamos pensar aqui: a raiz deve ser sempre positiva, certo? Do contrário teremos um número complexo, o que não cabe para essa função aqui. Então:

4 - y 2 ≥ 0

Veja também que o valor máximo para essa raiz é quando y = 0 , ou seja:

4 - 0 2 = 4 = 2 é o máximo que essa raiz pode atingir (porque o y 2 está negativo, então qualquer valor aí vai diminuir a raiz)

Ou seja, a gente tem que:

0 ≤ 4 - y 2 ≤ 2

Então, se a gente somar 1 em todos os pedacinhos da relação aqui em cima, temos mais ou menos isso aqui:

1 ≤ 1 + 4 - y 2 ≤ 3

E aí chegamos na nossa função, então a imagem é:

I m   F = [ 1,3 ]

Uhul! Conseguimos!

Pra essa questão é isso, pessoal!! Bora resolver mais uma?

Resposta

a) F 3,1 = 1 + 3

b) D = { x , y | 4 - y 2 ≥ 0 } → { ( x , y ) | x ∈ R ,   y ∈ - 2,2 }

c) I m F = [ 1,3 ]

Exercícios de Livros Relacionados

37. Para as funções de uma variável, é impossível uma função continua ter dois pontos de máximo local e nenhum ponto de mínimo local. Para funções de duas variáveis, esse caso existe. Mostre que a fun