Uma barra de ferro foi remendada segundo o ângulo mostrado na figura. Sabendo que ela será submetida aos esforços mostrados determine quais tensões apareceram no plano da emenda.
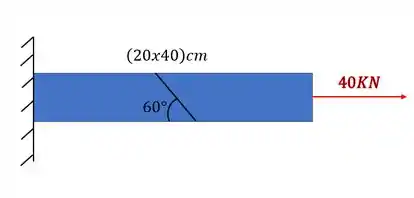
Passo 1
Vamos representar o nosso elemento infinitesimal de forma a trocar a nossa barra por um elemento que simbolize a ação do carregamento. Dessa forma teremos que o nosso elemento infinitesimal será
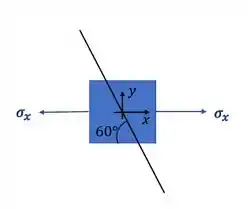
Também devemos rotacionar o nosso elemento de forma que a parede lateral do quadrado fique paralela a emenda da barra, que é exatamente o nosso plano orientado a 60°, logo as possíveis posições do nosso elemento serão
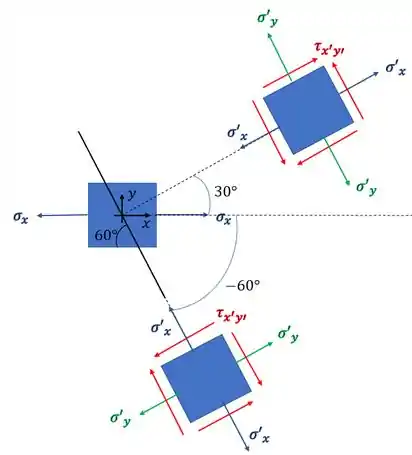
Passo 2
Sabemos também que as fórmulas que nos permitem calcular as tensões nesse plano são dadas por
Em que o nosso elemento apresenta apenas e .
Passo 3
Olhando novamente a nossa barra, teremos que
Sabemos que
Em que
Substituindo teremos que
Agora que temos todos os valores, vamos substituir na nossa fórmula.
Passo 4
E vamos testar para dois ângulos, primeiro com e depois com
Passo 5
Primeiro com
Primeiro com
Redesenhando o nosso elemento com as tensões encontradas teremos o seguinte estado de tensões
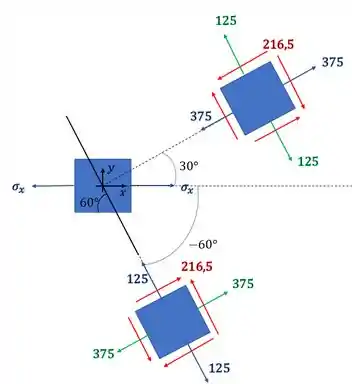
Marcando no desenho o plano que nos interessa teremos que
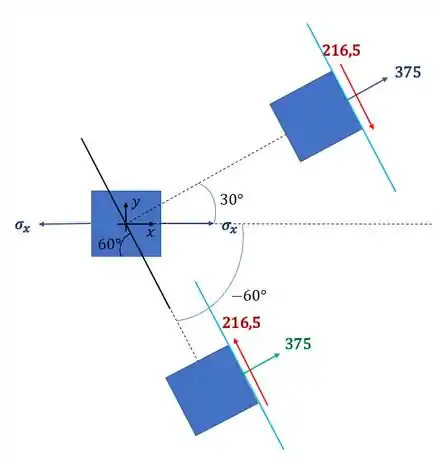
Podemos ver que a tensão que age no plano da emenda é dada pelas tensões que agem no plano azul do nosso desenho, assim podemos dizer que