Determine o estado de tensões de um elemento infinitesimal orientado de 79° no sentido horário.
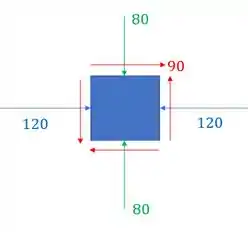
Passo 1
Aqui é importante entender o que está ocorrendo, a figura abaixo demonstra o que o enunciado fala
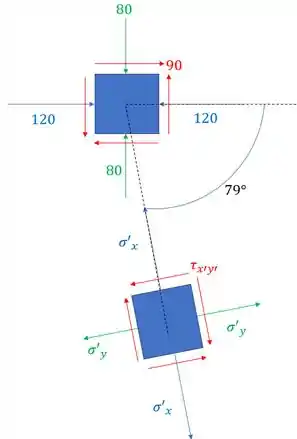
Sabemos então que se trata de uma simples transformação de tensão, que sabemos que devemos usar as seguintes fórmulas para determinar o estado de tensões do elemento que está a 79°. Aqui vale ressaltar um ponto muito importante, todos os ângulos em transformação de tensões que giram no sentido horário entram na fórmula com sinal negativo.
Passo 2
Agora que já sabemos qual o problema e quais fórmulas devemos usar, vamos ir encontrando cada valor do nosso elemento quando orientado a 79°
Sabemos que
Substituindo os valores em cada uma das equações teremos que
Passo 3
Passo 4
Passo 5
Passo 6
Passo 7
Passo 8
Redesenhando o elemento no novo estado de tensões teremos que
