Para o estado de tensão mostrado, determine: o valor de para o qual a tensão de cisalhamento no plano da cola seja zero e a tensão normal correspondente.
Passo 1
O que está acontecendo?
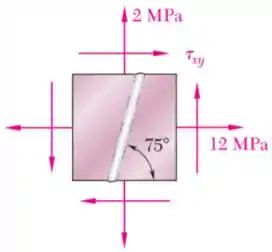
O elemento da figura possui um estado plano de tensões com:
- ;
- ;
- & desconhecido.
E o que é que o exercício quer saber?
Na letra , ele quer saber qual deve ser o valor de para que a tensão de cisalhamento no plano da cola seja zero.
Então devemos tentar descrever a tensão de cisalhamento no plano da cola!
Fazendo isso, vamos poder igualar essa tensão a zero e descobrir qual é o valor de correspondente.
Já na letra , o exercício quer saber qual vai ser a tensão normal no plano da cola tendo em mente esse caso proposto no item .
Então, para resolver o exercício...
Temos que fazer uma transformação de tensões nesse elemento com o objetivo de descrever a tensão de cisalhamento no plano da cola.
Isso envolve:
1. Definir um ângulo (positivo se for sentido anti-horário) de rotação que faça com que uma face do nosso elemento fique paralela ao plano da cola.
2. Aplicar a fórmula da transformação de tensões para a tensão de cisalhamento, usando esse ângulo definido no passo anterior:
& 3. Igualar essa fórmula a zero, de tal forma que a gente possa isolar e descobrir qual deve ser seu valor.
Depois que isso tiver sido feito, vamos poder seguir para o item , em que devemos:
1. Identificar se a tensão normal no plano da cola vai corresponder à tensão ou do elemento rotacionado.
(Isso depende do ângulo que tivermos escolhido.)
& 2. Aplicar a fórmula correspondente de transformação de tensões para a tensão normal:
Passo 2
Então vamos começar definindo a rotação do nosso elemento.
Uma opção é rotacionar ele com um ângulo , fazendo com que sua face direita fique paralela ao plano da cola:
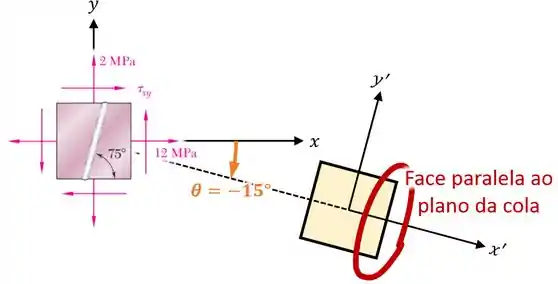
E assim está definida a nossa rotação!
Passo 3
Agora que já definimos a rotação , podemos aplicar a fórmula da transformação de tensões para a tensão de cisalhamento:
Aí, substituindo , & , essa fórmula fica assim:
Daí que, calculando tudo isso, encontramos que:
Passo 4
Descrita a tensão de cisalhamento no plano da cola, podemos agora igualá-la a zero para encontrar a tensão de cisalhamento original necessária para satisfazer essa condição.
Fazendo isso, vamos ter:
Isolando , encontramos que:
O que dá:
Que é a nossa resposta para a letra .
Passo 5
Agora, para a letra , podemos olhar de novo para a rotação que definimos:
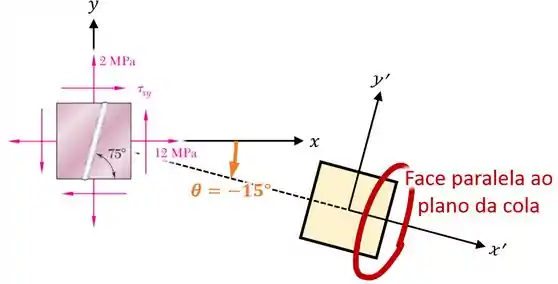
Olhando para essa imagem, vemos que:
A tensão normal que vai atuar no plano da cola deve ser a mesma tensão normal que atua na face paralela ao plano da cola, que é a tensão na direção .
Dessa forma, temos que a tensão normal no plano da cola vai ser dada pela fórmula:
Daí que, substituindo nessa fórmula , , & , ela fica assim:
Calculando tudo isso, encontramos que:
Ou seja, a tensão normal no plano da cola é uma tensão de tração de .