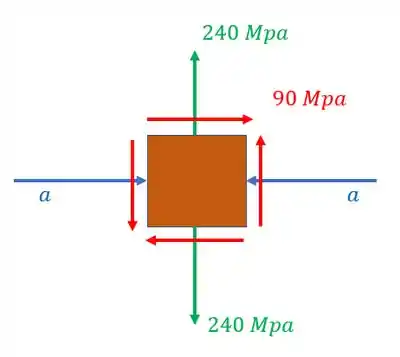
O elemento infinitesimal abaixo está sujeito aos esforços mostrados. Determine quanto deve valer a tensão no eixo x para que a tensão em x e em y sejam iguais quando o elemento estiver rotacionado de 22,5° no sentido anti-hor��rio.
Passo 1
Aqui é importante entender o que está ocorrendo
Sabemos que devemos garantir que as tensões no estado transformado sejam iguais, como sabemos que as fórmulas são
Basta que igualemos essas tensões para sabermos o que deveremos fazer, fazendo isso teremos que
Cortando a média das tensões teremos que
Isolando teremos que
Como queremos isolar o valor de x teremos que
Passo 2
Agora que já temos a nossa fórmula basta que substituamos os valores, com isso teremos que
Vamos substituir na equação que encontramos antes
Agora vamos testar para ver se de fato fizemos correto.
Passo 3
Usando a nossa fórmula teremos que
Logo de fato fizemos o cálculo correto e de fato na orientação 22,5° temos que a tensão no eixo x seria
Que quando orientado terá