Dado o elemento infinitesimal abaixo, determine o ângulo em que a tensão no eixo x será o quíntuplo da tensão cisalhante somado a tensão no eixo y.
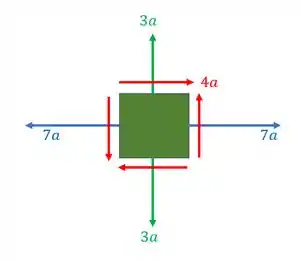
Passo 1
Aqui é importante entender o que está ocorrendo
Sabemos que devemos garantir que as tensões no estado transformado e no eixo x sejam iguais ao quíntuplo das tensões cisalhantes somado a tensão no eixo y, como sabemos que as fórmulas são
Passo 2
Basta fazermos a igualdade que foi mencionada afim de que essas tensões sejam iguais, para isso faremos
Cortando as médias de ambos os lados teremos que
Isolando tudo de um lado teremos que
Além da fórmula sabemos que
Substituindo na nossa equação teremos que
Isolando a tangente teremos que
Isolando o valor dos ângulos teremos que
Agora que já determinamos o nosso ângulo, vamos testar na nossa fórmula para vermos se fizemos os cálculos corretamente.
Passo 3
Usando a nossa fórmula teremos que
Vamos testar os valores na nossa fórmula para sabermos se os cálculos estão ok
Como o valor que calculamos foi
Vemos que a pequena diferença acontece pelas aproximações que fizemos, como conseguimos provar que de fato os nossos cálculos estão corretos, conseguimos determinar o ângulo que satisfaz a nossa equação que nesse caso é