Determine o estado de tensão equivalente em um elemento, se ele estiver orientado a em sentido anti-horário em relação ao elemento mostrado. Use as equações de transformação de tensão.
Passo 1
O que está acontecendo?
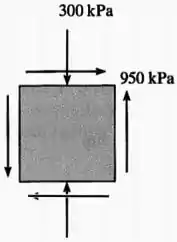
A imagem apresenta um estado plano de tensões em que:
- , uma vez que não há nenhuma tensão normal na horizontal;
- , com valor negativo uma vez que a tensão normal na vertical é de compressão;
- , com valor positivo uma vez que as setas da tensão cisalhantes está apontando para o 1° e 3° quadrante:
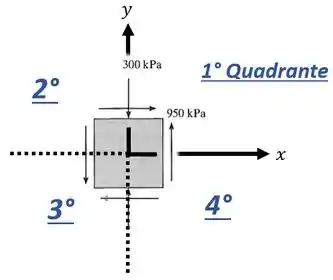
E o que é que o exercício quer?
Ele quer que a gente determine o estado de tensão , e nesse elemento caso os seus eixos sejam rotacionados por um ângulo em sentido anti-horário ():
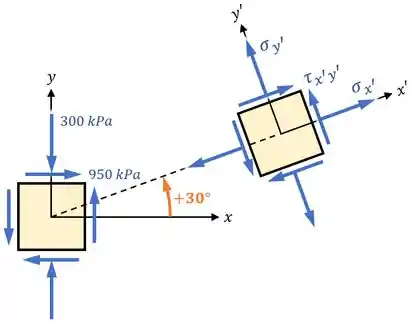
Para tanto, ele quer que a gente use as equações de transformação de tensões:
Então, para resolver esse exercício...
O primeiro passo é fazer o desenho que acabamos de fazer do elemento rotacionado.
O segundo é aplicar as equações de transformação de tensões.
E o terceiro é colocar os resultados encontrados no desenho do elemento rotacionado.
Com uma observação:
Caso o exercício pedisse somente as tensões , e , esse terceiro passo poderia ser pulado.
Mas como ele pediu que a gente determine o “estado de tensões equivalente”, imagina-se que ele quer que a gente faça um desenho desse estado de tensões.
Sendo que no geral, é sempre bom fazer esse desenho final mesmo. 😉
Passo 2
Então vamos lá!
Já fizemos no passo anterior um desenho do nosso elemento rotacionado, o que nos ajudou a identificar corretamente o ângulo .
Agora, é só uma questão de aplicar as fórmulas da transformação de tensões:
Substituindo nessas equações os valores:
- ;
- ;
- ;
- & ,
Elas vão ficar assim:
Aí, calculando essas expressões, vamos encontrar que:
Passo 3
No passo anterior, já encontramos as respostas do nosso exercício, mas para complementar a nossa solução, podemos desenhar essas tensões no nosso elemento rotacionado.
Para tanto, podemos perceber que:
- As tensões e , por serem positivas, vão ter seus sentidos convencionais no desenho.
- Já a tensão , negativa, vai ser representada no desenho somente com sua intensidade de , mas com um sentido oposto do convencional, ou seja, com o sentido de compressão.
Dessa forma, o estado plano de tensões para o nosso elemento rotacionado fica assim:
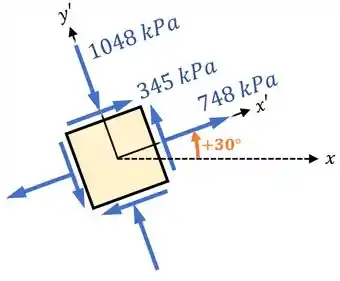
E pronto!
Está resolvido o exercício.