um garoto sofreu um acidente em que o osso do seu braço teve quer ser colado segundo o ângulo mostrado na figura. Sabendo que esse garoto foi jogar bola e sofreu uma entrada em que o osso do seu braço foi submetido aos esforços mostrados na figura. Sabendo que a tensão máxima cisalhante suportada no plano de rompimento é de 50KPa, determine se a entrada sofrida pelo garoto será suficiente para causar novamente o rompimento do seu osso.
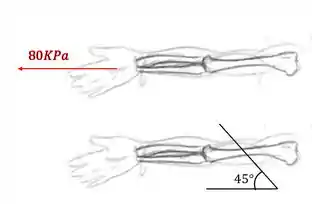
Passo 1
Vamos representar o nosso elemento infinitesimal de forma a trocar o nosso braço por um elemento que simbolize a ação da entrada no jogo de futebol. Dessa forma teremos que o nosso elemento infinitesimal será
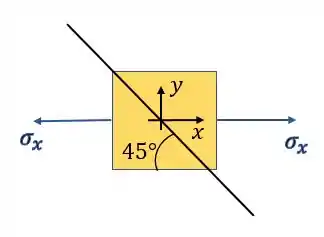
Também devemos rotacionar o nosso elemento de forma que a parede lateral do quadrado fique paralela a colagem do osso, que é exatamente o nosso plano orientado a 45°, logo as possíveis posições do nosso elemento serão
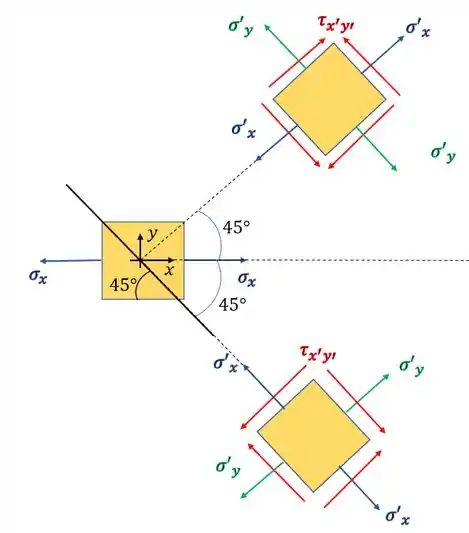
Passo 2
Sabemos também que as fórmulas que nos permitem calcular as tensões nesse plano são dadas por
Em que o nosso elemento apresenta apenas e .
Passo 3
Olhando novamente o nosso braço, teremos que
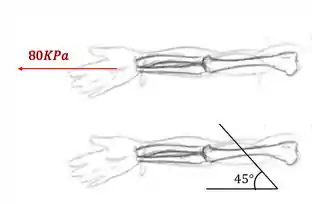
Sabemos que
Agora que temos todos os valores, vamos substituir na nossa fórmula.
Passo 4
E vamos testar para um único ângulo de
Passo 5
Com
Redesenhando o nosso elemento com as tensões encontradas teremos o seguinte estado de tensões
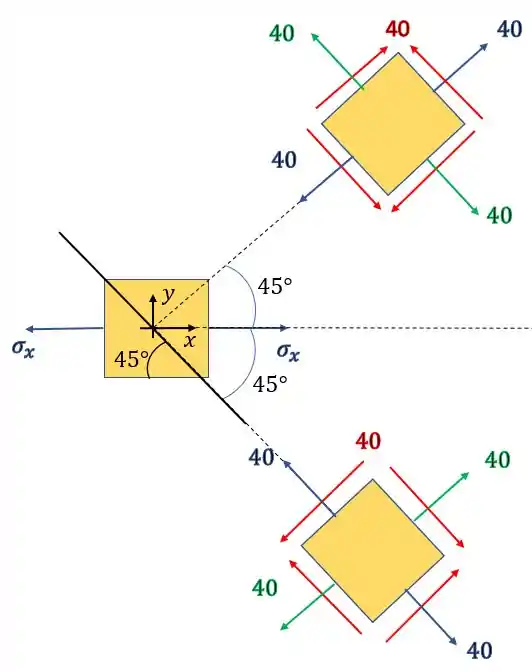
Marcando no desenho o plano que nos interessa teremos que
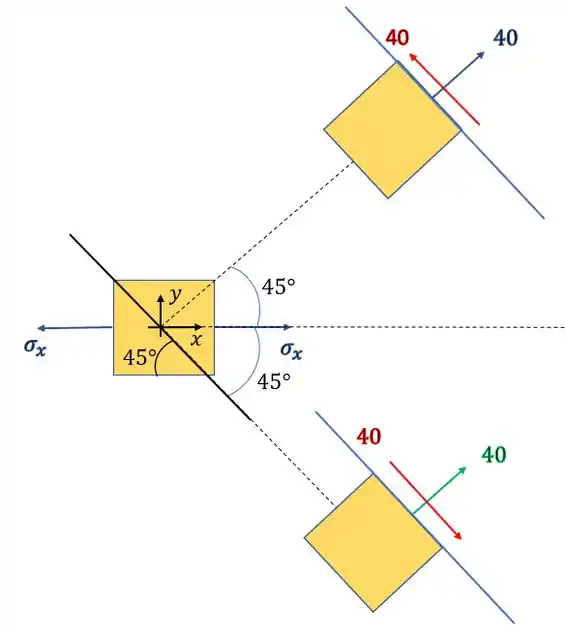
Podemos ver que a tensão que age no plano da emenda é dada pelas tensões que agem no plano azul do nosso desenho, assim podemos dizer que
Mas o objetivo da questão era saber se a entrada sofrida pelo garoto seria o suficiente para que novamente o braço do menino voltasse a quebrar-se.
Como foi dito no enunciado a resistência no plano era de 50KPa, como a tensão cisalhante no plano é de 40KPa podemos afirmar que não ocorrerá ruptura no braço do menino.
Resposta
A entrada sofrida pelo garoto não será suficiente para romper novamente o osso de seu braço, isso pois a resistência no plano de emenda é de 50KPa, enquanto que a máxima tensão cisalhante ocorrida no plano é de 40KPa.