UNICAMP - (Cálculo 3) - P1 2020.1
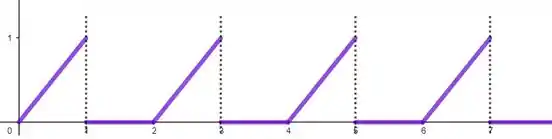
Considere a função de período dada por
Desenhe o gráfico de e calcule a transformada de Laplace . Justifique todas as propriedades da tabela de Transformadas de Laplace usadas.
Passo 1
Fala galera, bora começar! Antes de mais nada, vamos desenhar nossa função. Ela é uma rampa até o valor e depois zera, e repete esse comportamento de em diante. Vamos ter então:
A questão já da uma dica bacana pra gente: é uma função periódica. Só tem uma propriedade que nos ajuda nesses casos, que é essa aqui:
Portanto, sendo o período , já adiantamos que:
Po galera, mas como:
Podemos dividir a integral em dois pedaços pra levar em consideração cada uma das leis de formação de , de forma a ficar com:
Show, falta só resolver essa integral. Bora fazer isso no próximo passo?
Passo 2
Show galera, olha só, em:
Temos um produto de funções de tipos diferentes! Isso tem cheiro de integração por partes. Então se escolhermos, por exemplo:
Pela técnica de integração por partes, a integral:
Vai ficar:
Sendo que a integral a direita que sobrou na verdade já fizemos antes, quando transformamos em , então seu resultado sai direto:
A transformada vai ser então:
Resposta
