Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformada de Laplace da Função Degrau

Ver Teoria
Exercício 31245678910111213141516171819202122

Enunciado

Esboce o gráfico da função dada no intervalo t ≥ 0 e encontre sua transformada de Laplace.

f t = t - 3 u 2 t - t - 2 u 3 ( t )

Passo 1

Vamos primeiro desenhar essa função. Temos o seguinte:

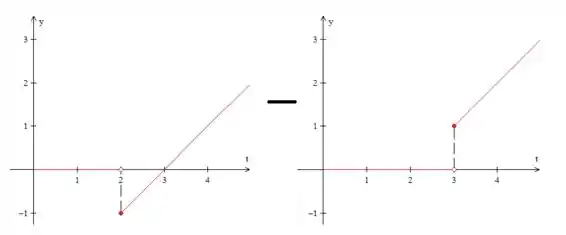
Juntando todas essas informações, temos:

  1. De 0 a 2 , y = 0 - 0 = 0
  2. De 2 a 3 , y = t - 3 - 0 = t - 3
  3. De 3 em diante, y = t - 3 - t - 2 = - 1

Temos, então, o seguinte gráfico:

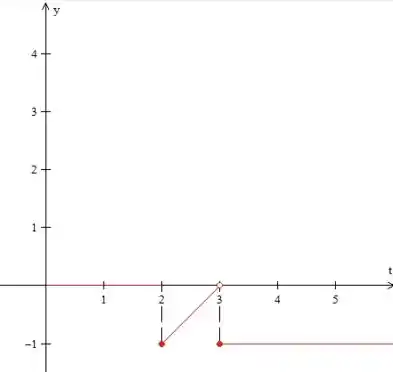
Passo 2

Agora vamos calcular a transformada dessa função.

L t - 3 u 2 t - t - 2 u 3 ( t ) s = L ( t - 3 ) u 2 t s - L ( t - 2 ) u 3 t s

Sabemos que

L u c f t - c s = e - c s L f t ( s )

  1. Para a primeira transformada

    2. L ( t - 3 ) u 2 t s = e - 2 s L f t ( s )

    Temos

    f t - 2 = t - 3

    Logo

    f t = t + 2 - 3 = t - 1

    Isso nos dá

    L ( t - 3 ) u 2 t s = e - 2 s L t - 1 ( s )

  2. Para a segunda transformada

L ( t - 2 ) u 3 t s = e - 3 s L f t ( s )

Temos

f t - 3 = t - 2

Logo

f t = t + 3 - 2 = t + 1

Isso nos dá

L ( t - 2 ) u 3 t s = e - 3 s L t + 1 ( s )

Passo 3

Temos, então, o seguinte:

L f t s = e - 2 s L t - 1 s - e - 3 s L t + 1 ( s )

Vamos resolver essa expressão.

L t - 1 s = 1 s 2 - 1 s = 1 - s s 2

L t + 1 s = 1 s 2 + 1 s = 1 + s s 2

Substituindo esses valores:

L f t s = e - 2 s 1 - s s 2 - e - 3 s 1 + s s 2

Resposta

e - 2 s 1 - s s 2 - e - 3 s 1 + s s 2