Encontre a transformada de Laplace da função dada.
Passo 1
Precisamos escrever em função de , para podermos calcular a transformada.
Vamos primeiro desenhar essa função:
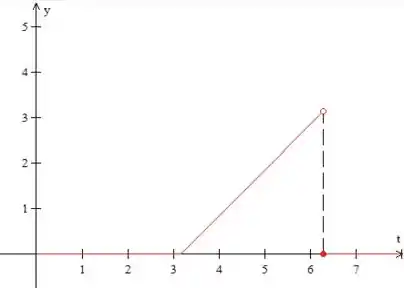
Repare que isso é o mesmo que:
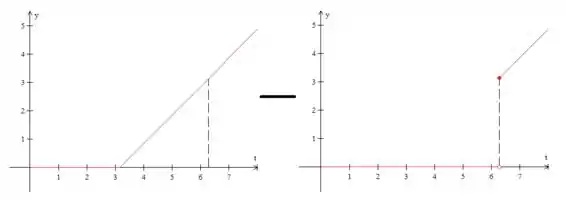
A função da figura da esquerda vale zero até e depois tem valor igual à equação da reta, , então, podemos escrevê-la como .
A função da direita vale zero até e depois vale . Então, podemos escrevê-la como .
Como a função do problema é a diferença entre essas duas, temos:
Precisamos calcular a transformada disso aí agora. Como temos dois ’s diferentes, vamos calcular cada transformada separadamente.
Passo 2
- Para
- Para
Precisamos encontrar a partir de . Temos a seguinte fórmula:
Sabemos que
Para se tornar , temos que substituir por , não é? Então vamos somar onde tem , olha só:
Pronto, descobrimos , agora basta substituir na fórmula:
Precisamos encontrar a partir de . Temos a seguinte fórmula:
Sabemos que
Para se tornar , temos que substituir por , então vamos fazer isso para os dois lados da equação:
Pronto, descobrimos , agora basta substituir na fórmula:
Nota: Cuidado! As duas funções degrau e estavam multiplicadas pela mesma função , mas a que encontramos para cada uma delas era diferente. Isso acontece porque para cada caso chamamos essa função de e esse “” não é o mesmo nos dois casos.
Passo 3
Temos, então:
Agora é só calcular as transformadas!
Substituindo esses valores, temos: