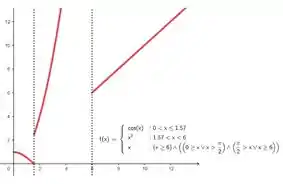
Dada:
Desenhe o gráfico de (não se preocupe com escala). Expresse usando funções escada . Utilizando a expressão da função encontrada, calcule a transformada de Laplace . Justifique todas as propriedades da tabela de Transformadas de Laplace usadas.
Passo 1
Eaiii povo, tudo na paz? Vamos lá! Pra começar, vamos lembrar que:
Dessa forma, pra escrever cheio de terminhos como esse, vamos ter que aproveitar de artimanhas parecidas com essa:
Bom, então uma boa primeira ideia , já que temos:
Fazer:
Um cuidado com isso, no entanto, porque na reta real, isso significa que temos:
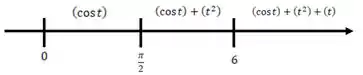
E queremos isso na real:
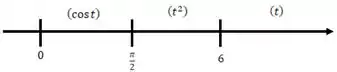
Então pra compensar, a partir de , tenho que remover o e a partir de , tenho que remover o . Pra fazer isso basta adicionar termos negativos que considerem essa remoção:
O que resulta em:
Pra confirmar que isso ta certo, podemos fazer as retas reais desses carinhas:
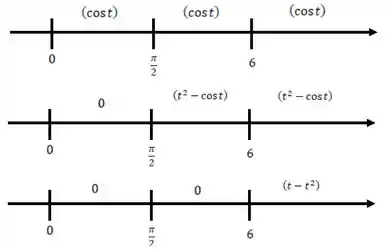
Note que a soma desses três dá exatamente o nosso :
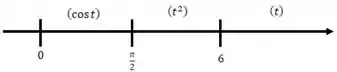
Usando a ideia da reta real, fazer o esboço de fica beeem mais tranquilo, saca só:
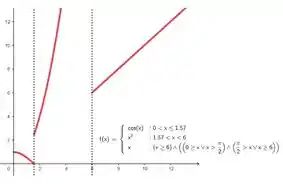
Passo 2
Pra gente fechar tudo falta só ver a transformada dessa função doida. Em todos os casos, vamos acabar usando essa propriedade:

Assim, seja:
Vamos ter:
Onde:
Falta só a gente achar e partimos pro abraço, vamos lá! Pra começar, temos o primeiro caso que é bem direto, já que . Nesse caso, usando a propriedade , temos:
![]()
Pro segundo caso, vamos ter que se:
Então:
E de propriedades trigonométricas, ao mesmo tempo abrindo o quadrado ao lado, temos:
E pra fazer a transformada desse cara, temos que usar as seguintes propriedades:
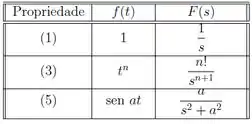
Sendo assim, ficamos com esse cara bacana aqui:
Pra fechar falta só achar . Galera, sem mistério, mesmíííííssima ideia. Então se:
Vamos ter:
Juntando os termos:
A transformada inversa vai usar as propriedades e mostradas na foto anterior, ok? Bora lá!
Passo 3
Pra gente fechar tudo tudinho mesmo, falta só juntar. Início do passo passado (hahaha soou engraçado), achamos:
Ai precisamos achar e achamos! Eles eram:
Juntando isso ai tudo, temos:
Resposta