Um reservatório tem dimensões de e contém água até a sua metade. O número de litros de água contido é um valor próximo de:
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí, pessoal!!
Ele diz pra gente que tem um reservatório:
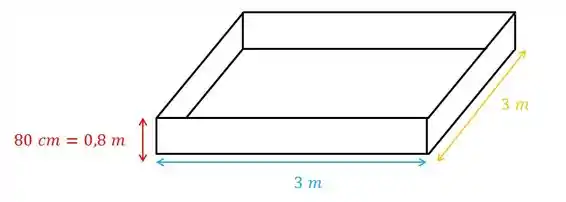
Vamos calcular o volume desse reservatório! E atenção!! Tem o ali, eu já transformei direto pra metro que aí fica tudo no SI, beleza?
Pra gente converter de pra litro é só usar essa relação:
Então, fazendo uma regra de três:
Resolvendo isso daí:
Show, esse é o volume do reservatório todo!
Mas ele tá cheio de água? Não né!
Tem água só até a metade,
então o volume de água dentro dele é:
Resposta
Alternativa D.