Quais são as unidades de volume? Suponha que um aluno diga que o volume de um cilindro com altura e raio seja dado por . Explique por que isto está errado
Passo 1
Para descobrir as unidades de volume podemos pegar um volume simples de calcular para analisar, como o volume de um cubo por exemplo.
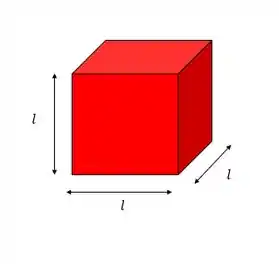
O cubo possui 3 lados iguais e nesse caso como a gente faz pra calcular o volume?
Passo 2
Para calcular o volume de um cubo temos:
Passo 3
Como a dimensão de cada lado é um comprimento linear a gente pode dizer que um lado tem a dimensão de um comprimento , ou seja, sempre será uma medida de comprimento como por exemplo: milímetros, centímetros ou metros.
Logo se calculamos o volume do cubo que é lado ao cubo, temos também a sua dimensão que é:
Sendo assim a unidade do volume do cubo é comprimento ao cubo:
Passo 4
Como o volume de um cubo tem a mesma dimensão que qualquer outro volume temos que:
Passo 5
Considerando um volume de um cilindro como , vamos analisar dimensionalmente essa fórmula:
Passo 6
Assim o volume do cilindro seria:
Cara mas e aí, é possível que o volume tenha uma dimensão de Como vimos o volume tem dimensões cúbicas do tipo , então não seria possível esse volume pro cilindro então a afirmativa é falsa.