Exercícios de Análise Dimensional e de Unidades - Lista de Exercícios Resolvida

Quais são as unidades de volume? Suponha que um aluno diga que o volume de um cilindro com altura e raio seja dado por . Explique por que isto está errado

Força tem dimensões de massa vezes aceleração. Aceleração tem dimensões de rapidez divida por tempo. Pressão é definida como força dividida por área. Quais são as dimensões da pressão? Expresse a pressão em termos das unidades básicas do SI quilograma, metro e segundo.

A lei de decaimento radioativo é onde é o número de núcleos radioativos em , é o número de núcleos radioativos no tempo e é uma quantidade conhecida como a constante de decaimento. Qual é a dimensão de ?

A terceira lei de Kepler relaciona o período de um planeta com o raio de sua órbita , a constante da lei de Newton da gravitação () e a massa do sol . Qual a combinação destes fatores fornece as dimensões corretas para o período de um planeta ?

1. A unidade SI de força, o quilograma-metro por segundo ao quadrado (), é chamada de Newton . Encontre as dimensões e as unidades SI da constante G na lei de Newton da gravitação,
2. A quantidade de movimento de um objeto é o produto de sua velocidade pela sua massa. Mostre que a quantidade de movimento tem as dimensões de força multiplicada pelo tempo.

Nas equações seguintes, a distância está em metros, o tempo está em segundos e a velocidade está em metros por segundo. Quais são as unidades SI das constantes e ?

A posição de uma partícula que se move no eixo varia com o tempo segundo a equação . Sabendo que as unidades de e são e , respectivamente, as dimensões das grandezas e são, respectivamente:

(a)

(b)

(c)

(d)

(e) Nenhuma das outras respostas.

Um reservatório tem dimensões de e contém água até a sua metade. O número de litros de água contido é um valor próximo de:

(a)

(b)

(c)

(d)

(e)

A velocidade é uma grandeza derivada de outras duas grandezas, no SI é expressa em e que,de acordo com o conceito de análise dimensional,expressa a razão:

a) comprimento / tempo

b) velocidade / tempo

c) massa / tempo

d) temperatura / tempo

e) massa / temperatura

Dada uma grandeza obtida a partir de outras e tal que e supondo que tenha dimensão dada por , tenha dimensão e tenha dimensão , os valores de e são ( representa a dimensão de comprimento e representa a dimensão de tempo):

a. e ;

b. e

c. e

d. e

e. e

Se tem unidades de e tem unidades de , quais as unidades de , se ?

a)

b)

c)

d)

e)

Substâncias altamente explosivas depositam uma grande quantidade de energia quase que instantaneamente em um pequeno volume. É postulado que o raio da onda de choque esférica resultante no momento após o a explosão deve depender principalmente da energia liberada e da densidade do ar não perturbada . Encontre essa relação.

Suponha que , onde tem dimensões , tem dimensões e tem dimensões . Então os expoentes e têm respectivamente os valores:

a) e ;

b) e ;

c) e ;

d) e ;

e) e ;

Suponha que , onde A tem dimensões , B tem dimensões e C tem dimensões . Então os expoentes e têm, respectivamente, os valores:

A. e

B. e

C. e

D. e

E. e

(Cap 1 – Ex 23) Nas equações a seguir, a distância está em metros, o tempo está em segundos, e a velocidade está em metros por segundo. Quais são as unidades do SI das constantes e ? (a) , (b) , (c) , (d) , (e) .

Classifique como (V) verdadeiras ou (F) falsas as afirmações abaixo, e assinale a alternativa correta:

() Uma velocidade tem dimensão de comprimento por tempo, e sua unidade no SI é metro/hora.

() Dimensão é a mesma coisa que unidade.

() Quantidades adimensionais (ou sem dimensão) necessitam da especificação de uma unidade para estarem bem definidas.

() Uma equação verdadeira não precisa ser dimensionalmente consistente.

1. FFFF
2. VVFV
3. FVVF
4. FFVV
5. FFFV

A força de resistência do ar sobre uma massa obedece à equação , onde é a velocidade da massa, para o intervalo de velocidades estudado em um experimento. Um gráfico de (em ) em função de (em ) é mostrado abaixo. Qual é o valor aproximado de ?

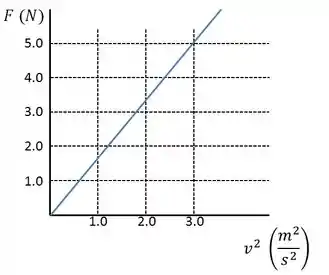
A.

B.

C.

D.

E.

(Medição e Arredondamento) Indique como os seguintes resultados devem ser relatados. Explique.

c) Uma medida de intervalo temporal resultou em e .

(Medição e Arredondamento) Indique como os seguintes resultados devem ser relatados. Explique.

1. Um conjunto de medidas de corrente elétrica resultou em um valor médio de com desvio padrão (da média) de . O manual do amperímetro estabelece a incerteza de para medidas na faixa de correntes de e incerteza de na faixa de .

(Medição e Arredondamento) Indique como os seguintes resultados devem ser relatados. Explique.

b) Com o mesmo amperímetro do item anterior, outro experimento (completamente distinto) obteve um conjunto de medidas com e .

Uma partícula de massa está se movendo sobre atuação de uma força que depende de sua velocidade. A força é dada por:

onde e são constantes positivas e é a magnitude da velocidade da partícula. Se no tempo , a partícula está se movendo a uma velocidade de magnitude descubra a função da magnitude da velocidade com o tempo. Use as constantes mencionadas no problema. Supondo que a equação adote o Sistema Internacional de unidades, qual seria as unidades das constantes e variáveis mencionadas no problema?

Para ilustrar o conceito de uma “equação quantitativa” (proposta por Lira, Ignacio, Eur. J. Phys. 34, 2013, 1391-1401) considere a relação entre a aceleração padrão de queda livre, , e o tempo leva um corpo a cair uma distância a partir do repouso. Na ausência de efeitos viscosos, a equação de quantidade é simplesmente , que é equivale à sua forma adimensional . Agora suponha que essa equação não seja conhecida; é meramente conjeturado que, se as forças de arrasto e empuxo forem insignificantes, deve haver uma relação entre e a massa do corpo: . Obtenha uma expressão adimensional equivalente, tomando cada dimensão base, uma por vez, e elimine-a multiplicando as quantidades que contêm essa dimensão por uma quantidade arbitrariamente selecionada que também contenha a dimensão, elevada aos expoentes apropriados.