UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 10c
Um disco circular isolante e fino, de raio , tem uma densidade superficial, de raio , tem uma densidade superficial de carga dada por , onde é uma constante positiva e é a distância ao centro do disco.
- Considere agora que este ponto está muito longe do disco, de forma que . Determine uma expressão assintótica para o resultado do item anterior neste limite e interprete o resultado.
Passo 1
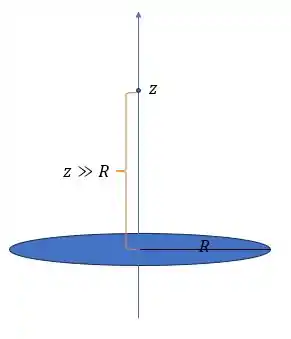
Eaee!!! Belezinha? Seguinte... a questão nos pede para calcular o vetor campo elétrico em um ponto localizado sobre o eixo perpendicular ao plano do disco e que passa pelo seu centro, a uma distância que se aproxima do infinito (quando comparado a ), ou seja:
Bom... a gente descobriu no item anterior que o campo elétrico em um ponto distante do disco é dado por:
Para aplicarmos para esse caso, onde é muito maior que , podemos fazer tender ao infinito.
Assim, basta aplicarmos esse conceito a um limite e analisar seu resultado!
E aí? Bora lá??
😉
Passo 2
Assim, aplicando no limite, temos:
Perceba que se encontra apenas no denominador e que, quando aplicamos o limite de , o resultado do campo elétrico tende a zero, ou seja:
E isso faz total sentido!!
Imagina aí... quando mais aumentarmos a distância do ponto , menos interferência do campo elétrico haverá nele!!
Entendeu direitinho? Responde aee ;)
