A que distância do eixo de um disco de plástico uniformemente carregado de de raio o módulo do campo elétrico é igual à metade do módulo do campo no centro do disco?
Passo 1
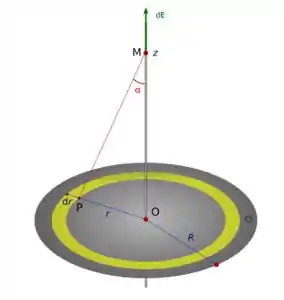
Observar que, no caso do disco, os componentes infinitesimais que devemos integrar são pequenas rosquinhas de largura e raio como a indicada em verde na figura acima.
A área infinitesimal dessas rosquinhas vale a derivada da área do círculo de raio em relação a :
Passo 2
Calcular a carga infinitesimal da região verde, multiplicando a pequena área pela densidade superficial de campo, que é constante pois o disco está uniformemente carregado.
Passo 3
Note que a resultante do campo elétrico se encontra no eixo , devido à simetria do problema. Isso por que dois pontos do anel radialmente opostos dão campos de mesma intensidades e que somados dão um campo na direção como na figura abaixo
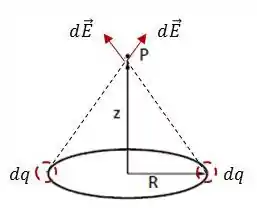
Então:
Passo 4
Determinar quem é o campo infinitesimal gerado por cada pedacinho verde da figura e substituir na equação encontrada.
Passo 5
Precisamos descobrir , para isso devemos projetar o campo infinitesimal do passo anterior no eixo .
Passo 6
Resolvendo a integral:
Agora o lance é resolver essa integral. GERALMENTE essa integral vem num formulário da sua prova, mas se não vier vamos ensinar aqui você a fazer! Pra isso pega aí aquela sua caneta/lapiseira/lápis especial e me acompanha, belê?
Passo 7
Primeiro de tudo, essa integral não sai direto! Pra isso temos que fazer uma substituição.
Olhando pra ela
Vamos ter que simplificar esse denominador. Como em cima tem um , a integral tá pedindo pra gente fazer a seguinte substituição
De forma que
E os limites de integração ficam
Então a nossa integral vai ficar
Essa integral vai ser
Assim a nossa integral fica
Finalmente
Voltando para o nosso campo
Supondo , vamos ter
Passo 8
Determinar o campo elétrico no centro do disco, que ocorre quando :
Queremos saber em que posição o campo vale a metade disso.
Passo 9
Logo: