Um elétron é liberado a partir do repouso no eixo central de um disco uniformemente carregado de raio . A densidade superficial de cargas do disco é . Determine o módulo da aceleração inicial do elétron se ele for liberado a uma distância do centro do disco de:
(a)
(b)
(c)
(d) Por que o módulo da aceleração quase não varia com a distância entre a carga e o disco?
Dado: Razão carga massa do elétron:
Passo 1
Temos a seguinte situação
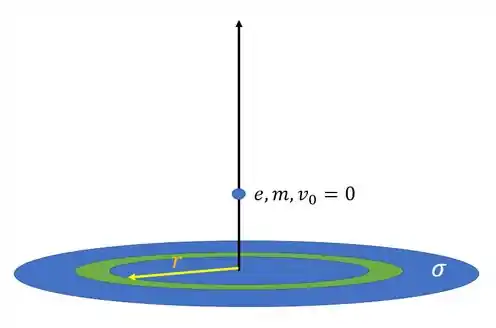
Observe que, no caso do disco, os componentes infinitesimais que devemos integrar são pequenas rosquinhas de largura e raio como a indicada em verde na figura acima.
A área infinitesimal dessas rosquinhas vale a derivada da área do círculo de raio em relação a :
Passo 2
Vamos calcular a carga infinitesimal da região verde, multiplicando a pequena área pela densidade superficial de campo, que é constante pois o disco está uniformemente carregado.
Passo 3
Notar que o campo elétrico resultante se encontra no eixo , devido à simetria do problema. Então:
Passo 4
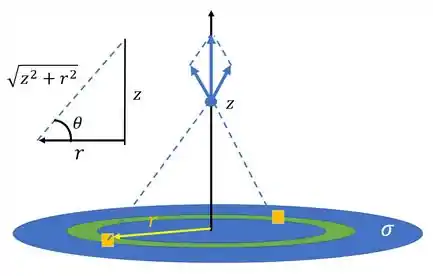
Temos que determinar quem é o campo infinitesimal gerado por cada pedacinho do disco carregado e substituir na equação encontrada.
Todos os pedacinhos do disco estão a uma distância do nosso ponto! Outro ponto importante é que devido a simetria o campo tem que apontar na direção . Para pegarmos essa componente basta multiplicar por que tá mostrado na figura acima, beleza?
Então temos
Pela figura
E já vimos que
Assim
Passo 5
Agora basta integrar!
Pra fazer essa integral é só fazer a substituição !
O resultado vai ser:
Passo 6
Podemos a partir do campo determinar a força, que é igual ao produto da massa do elétron pela aceleração que queremos determinar:
Logo:
Passo 7
Substituir os valores sugeridos no problema:
(a) Se
(b) Se
(c) Se
Passo 8
O módulo da aceleração quase não varia para menores distâncias entre a carga e o disco porque a resultante da força produzida pelas cargas próximas da borda do disco diminuir com a redução da distância entre o elétron e o centro do disco.
Quando a distância do elétron é muito menor que o raio do disco, o elétron “vê” esse disco como um plano infinito! Lembra como era o campo de um plano infinito? Ele não depende da distância da carga até o plano! A mesma coisa acontece aqui desde que a distância seja muito menor do que o raio do disco!
Outra forma mais matemática de ver isso é:
No limite , a gente pode fazer a razão tender a zero já que essa razão é um número muito pequeninho! Então nesse limite
Resposta
(a) Se
(b) Se
(c) Se
(d) O módulo da aceleração quase não varia para menores distâncias entre a carga e o disco porque a resultante da força produzida pelas cargas próximas da borda do disco diminuir com a redução da distância entre o elétron e o centro do disco.
Isso ocorre porque nessas posições essas forças quase se cancelam e apenas as cargas próximas ao centro do disco exercem influência no elétron.