Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campos Cruzados

Ver Teoria
Exercício 211234567891011121314151617181920222324

Enunciado

Considere um campo eletrostático representado pelas superfícies equipotenciais tracejadas e uma linha de campo elétrico contínua na figura abaixo.

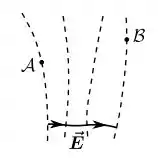
Quando um elétron é deslocado do ponto A para o ponto B , podemos afirmar que a diferença de potencial ∆ V = V   ( B ) - V   ( A ) à qual ele é submetido e o trabalho W e   A   →   B que a força elétrica realiza sobre ele satisfazem:

  1. ∆ V < 0     e     W e   A   →   B < 0
  2. ∆ V < 0     e     W e   A   →   B > 0
  3. ∆ V > 0     e     W e   A   →   B > 0
  4. ∆ V > 0     e     W e   A   →   B < 0
  5. ∆ V = 0     e     W e   A   →   B = 0

Passo 1

Cara... Para essa questão precisamos apenas de duas coisas...

  1. Saber que o campo elétrico sempre tem sentido de decaimento do potencial V , afinal o campo elétrico sempre é o negativo do gradiente do potencial...

    2. E → = - ∇ V

  2. O trabalho feito para se movimentar uma carga q de um ponto com potencial V A ao outro de potencial V B é...

W e   A   →   B = q V A - V B

Passo 2

Então veja bem, se o campo elétrico sai da esquerda e vai para a direita...

O potencial deve aumentar no sentido oposto, isto é o potencial de A ( V A ) deve ser maior que o potencial de B ( V B )...

V A > V B

Então...

V B - V A < 0

Logo...

∆ V = V B - V A = V B - V A < 0

Passo 3

Agora, o trabalho que vai ser realizado para movimentar uma carga - q (negativa) de A → B ...

W e   A   →   B = - q V A - V B

Só que pelo passo anterior...

V A > V B     →           V A - V B > 0

Logo, pelo fato de a carga ser negativa...

W e   A   →   B = - q V A - V B < 0

Resposta

Letra A

Exercícios de Livros Relacionados

Uma fita de cobre com 150 μ m de espessura e 4,5 m m de largura é submetida a um campo magnético uniforme B de módulo 0,65 T, com B perpendicular à fita. Quando uma corrente i = 23 A atravessa a fita,
Na Fig. 28-31, um elétron acelerado a partir do repouso por uma diferença de potencial V 1 = 1,00 k V entra no espaço entre duas placas paralelas, separadas por uma distância d = 20,0 m m , entre as q
Uma fita metálica com 6,50 c m de comprimento, 0,850 c m de largura e 0,760 m m de espessura está se movendo com velocidade constante v em uma região onde existe um campo magnético uniforme B = 1,20 m
Uma partícula com uma carga de 5,0μ C está se movendo em uma região onde existem um campo margnético de - 20 îm T î e um campo elétrico de 300 jV / m . Em um certo instante, a velocidade da partícula
O capacitor da Fig. 32-7 está sendo carregado com uma corrente de 2,50 A. O raio do fio é 1,50 mm e o raio das placas é 2,00 cm. Suponha que as distribuições da corrente i no fio e da corrente de desl