A figura abaixo mostra a trajetória de uma partícula de massa e carga que passa por uma região de campo magnético uniforme (acinzentada), onde ela descreve uma semicircunferência de raio .
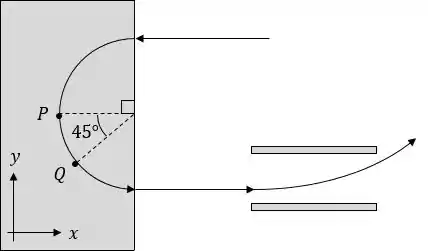
Depois de sair da região a partícula passa por entre duas placas paralelas eletricamente carregadas e é desviada no sentido da placa de maior potencial.
Qual é o sinal de ? Justifique.
Sabendo que a partícula entra na região de campo magnético uniforme com uma velocidade , qual é o vetor campo magnético na região acinzentada?
Calcule o vetor força magnética exercida sobre a partícula nos pontos e ;
Se a intensidade do campo elétrico na região entre as placas paralelas é , qual deveria ser o vetor campo magnético nessa região, para que a partícula não fosse desviada?
Passo 1
Qual é o sinal de ? Justifique.
O enunciado nos diz que, ao passar entre as placas paralelas, a partícula é desviada para a placa de maior potencial.
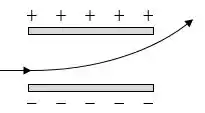
Assim, para ser desviada para a placa de maior potencial, a carga deve ser negativa.
Passo 2
Sabendo que a partícula entra na região de campo magnético uniforme com uma velocidade , qual é o vetor campo magnético na região acinzentada?
Ao longo da trajetória circular, a força magnética aponta sempre para o centro da trajetória. Assim, pegando o ponto assim que a partícula entra na região de campo magnético uniforme, temos que:
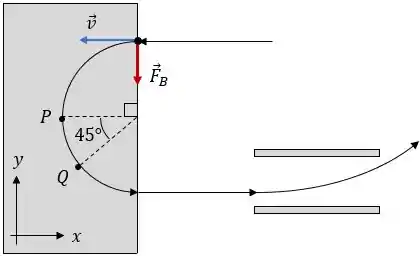
Sabendo que a força magnética sobre a partícula é dada por:
Como a partícula é negativa, o produto vetorial deve apontar no sentido contrário ao da força magnética.
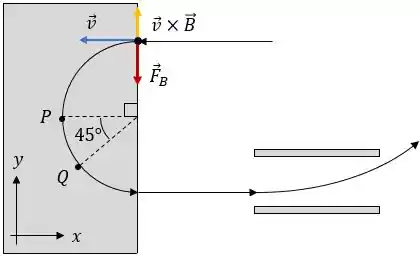
Assim, utilizando a regra da mão direita, onde o dedo indicado representa a velocidade e o dedo polegar indica o sentido de , o campo magnético deve ter o sentido .
Agora precisamos determinar a expressão para o módulo do campo magnético.
Passo 3
O raio da trajetória circular é dada por:
Reorganizando os termos, temos que:
Finalmente, o vetor campo magnético é dado por:
Passo 4
Calcule o vetor força magnética exercida sobre a partícula nos pontos e ;
No ponto , o vetor velocidade é dado por:
Assim, a força magnética será dada por:
Passo 5
No ponto , o vetor velocidade é dado por:
Assim, a força magnética será dada por:
Passo 6
Se a intensidade do campo elétrico na região entre as placas paralelas é , qual deveria ser o vetor campo magnético nessa região, para que a partícula não fosse desviada?
O vetor campo magnético deve gerar uma força contrária à força elétrica, ou seja, no sentido . Como estamos trabalhando com uma carga negativa, o produto vetorial deve ter o sentido .
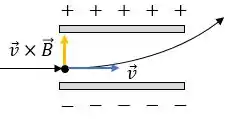
Assim, utilizando a regra da mão direita, onde o dedo indicado representa a velocidade e o dedo polegar indica o sentido de , o campo magnético deve ter o sentido .
Já o módulo do campo magnético está associado ao campo elétrico da seguinte forma:
Finalmente:
Resposta
Negativa.
Ponto :
Ponto :