Um elétron se movimenta em uma trajetória retilínea com velocidade na presença de um campo elétrico e de um campo magnético constantes. A componente da velocidade do elétron é:
Passo 1
Pra começar, vamos começar olhando para os vetores, dados por:
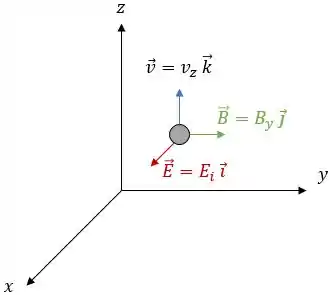
Como estamos trabalhando com um elétron, as forças magnética e elétrica terão os seguintes sentidos:
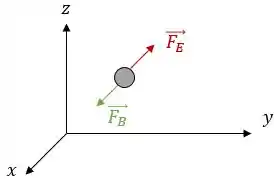
Como a trajetória é retilínea, a força resultante sobre o elétron é nula, sendo assim:
Resposta
Exercícios de Livros Relacionados
Uma fita de cobre com 150 μ m de espessura e 4,5 m m de largura é submetida a um campo magnético uniforme B de módulo 0,65 T, com B perpendicular à fita. Quando uma corrente i = 23 A atravessa a fita,
Na Fig. 28-31, um elétron acelerado a partir do repouso por uma diferença de potencial V 1 = 1,00 k V entra no espaço entre duas placas paralelas, separadas por uma distância d = 20,0 m m , entre as q
Uma fita metálica com 6,50 c m de comprimento, 0,850 c m de largura e 0,760 m m de espessura está se movendo com velocidade constante v em uma região onde existe um campo magnético uniforme B = 1,20 m
Uma partícula com uma carga de 5,0μ C está se movendo em uma região onde existem um campo margnético de - 20 îm T î e um campo elétrico de 300 jV / m . Em um certo instante, a velocidade da partícula
O capacitor da Fig. 32-7 está sendo carregado com uma corrente de 2,50 A. O raio do fio é 1,50 mm e o raio das placas é 2,00 cm. Suponha que as distribuições da corrente i no fio e da corrente de desl