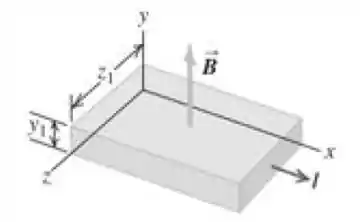
A Figura abaixo indica uma placa de prata com dimensões e e que produz uma corrente igual a no sentido . A placa está em repouso em um campo magnético uniforme na direção , cujo módulo é igual a . Sabendo que existem elétrons livres por metro cúbico, determine:
- o módulo da velocidade de arraste dos elétrons na direção do eixo ;
- o módulo, a direção e o sentido do campo elétrico no eixo produzido pelo efeito Hall ;
- a fem Hall.
Passo 1
a) Como a gente viu na teoria, a densidade de corrente na direção é dada por
Por outro lado, sabemos também que a densidade é a corrente por unidade de área. Por isso, podemos escrever também que
onde já usamos que a área por onde os elétrons fluem é , como está se pode ver na Figura, já que a corrente flui na direção e sentido do eixo .
Convertendo os valores necessários pro SI
E lembrando que a carga do elétron é
Colocando os valores dados no enunciado, temos
Passo 2
b) Como os elétrons estão caminhando na direção e sentido do eixo , então, a velocidade de arraste está na direção contrária, isto é,
Como o campo magnético é e a carga dos elétrons é negativa, temos que a força magnética é dada por
Portanto, a força magnética está ao longo do eixo . Nesse caso, então, a força elétrica deve estar no sentido do eixo . Como a força elétrica sobre os elétrons é dada por e essa força tem que ser igual a , o vetor campo elétrico tem que estar na direção do eixo .
Para encontrarmos o módulo de , temos que igualar a força elétrica com a força magnética. Isso dá para a gente o seguinte
O vetor campo elétrico é
Passo 3
c) Para fechar, a fem Hall, que está ao longo do eixo e é uma espécie de ddp ao longo da barra nessa direção, é dada por
Resposta
a)
b)
c)